
行測資料分析速算技巧
行測資料分析中不一樣的加減運算順序
近幾年行測考試中對于資料分析的加減法題目的選項往往呈現(xiàn)出一個跟以往不同的特點,就是選項中往往給出的是一個范圍,那在這種情況下,可能用老的套路只計算每個數(shù)的后幾位就很難快速判斷出到底應該選擇哪一個選項,基于這點,政華公考今天教給大家一種全新的加減法的計算思路——從高位開始計算。
我們從小學開始接觸加減運算,當時學校里面講到的加減運算是從后往前進行計算,例如:22875+52837+99865,如果我們列豎式計算的話,我們應該依次計算個位、十位、百位、千位和萬位,選擇從個位開始加和的原因是有可能會有進位或借位,從后往前計算會在計算這一位數(shù)的時候考慮到下一數(shù)位的進位或借位問題,但是當選項不適合用尾數(shù)開始計算時,我們可以從高位開始計算,兼顧到下一數(shù)位的進位和借位問題即可。
例題:25621+37124+72563=( )。
A.不到11萬 B.11萬~12萬之間
C.12萬~13萬之間 D.超過13萬
【答案】D【解析】對于這種題目如果用尾數(shù)法的話,我們得計算到倒數(shù)第5位之后才能判斷究竟應該在哪個范圍,基本上就相當于精算了。那應該怎么計算呢?觀察選項我們會發(fā)現(xiàn)選項之間的區(qū)別在于萬位這四個是各不相同的A選項是不到11萬,B是11萬多,C是12萬多,D是超過13萬,那也就說明其實我們只要知道最終結果的萬位數(shù)是幾就可以了,那如果要想知道萬位可以直接取原式三個數(shù)中萬位及以上數(shù)位上的數(shù)進行計算,即計算2+3+7=12萬,但是從首位開始計算時需要考慮下一數(shù)位的進位問題,也就是說萬位上的數(shù)=萬位加和+千位進位,此題千位加和為5+7+2=14,向萬位進1,那么萬位上的數(shù)就應該是12+1=13萬,故本題應該選擇D。
【小結】加法運算快速計算首幾位有效數(shù)字時,根據(jù)選項判斷需要精確計算的數(shù)位,將原式中該數(shù)位及以上數(shù)位上的數(shù)進行求和后加上下一數(shù)位的進位即可。
練習題:2015年-2018年A省人力資源專業(yè)畢業(yè)生人數(shù)分別為12921人、18982人、23654人、47191人。
問:2015年-2018年,A省人力資源專業(yè)畢業(yè)生總數(shù)為( )。
A.8萬~9萬 B.9萬~10萬
C.10萬~11萬 D.11萬~12萬
【答案】C【解析】問題所求為2015年-2018年畢業(yè)生總和,列式為12921+18982+23654+47191。根據(jù)選項可知,只要確定最終加和的萬位數(shù)即可,依據(jù)上面講過的方法,萬位加和+千位進位=最終結果的萬位數(shù)。萬位加和為1+1+2+4=8萬,千位進位為2+8+3+7=20進2,故最終結果的萬位數(shù)應該為8+2=10萬,選擇C選項。
通過以上題目的訓練,希望大家能夠了解對于加法運算當選項中給出的是范圍區(qū)間的話,快速確定首幾位有效數(shù)字會更容易得出結果。
行測資料分析速算技巧之特征數(shù)字法
在行測資料分析的學習過程中,計算方法的學習是非常關鍵的。掌握高效的計算技巧可以達到事半功倍的效果,在資料分析的計算中掌握特征數(shù)字法就很好的說明這一點,政華公考在此給大家介紹一下這種計算方法。
一、什么是特征數(shù)字法
特征數(shù)字法就是利用百分數(shù)和分數(shù)之間的相互轉化,將列式中的百分數(shù)近似地轉化成一些特定的分數(shù),從而達到簡化計算的一種方法。
二、常見百分數(shù)與分數(shù)之間的轉化

三、應用環(huán)境

【例1】2017年上半年,小微服務業(yè)樣本企業(yè)資產(chǎn)總計462.2億元,2018年比2017增長25.9%。
問題:2018年小微服務業(yè)樣本企業(yè)資產(chǎn)總計比2017年增長了( )億元?
A.108.2 B.119.7 C.123.5 D.130.6
【答案】【解析】根據(jù)材料可知,2017年上半年,小微服務業(yè)樣本企業(yè)資產(chǎn)總計462.2億元,2018年比2017增長25.9%。所求為 ,結果偏小選稍大的選項,本題選擇B項。
,結果偏小選稍大的選項,本題選擇B項。
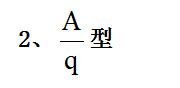
【例2】2018年,我國可再生能源發(fā)電量達1.87萬億千瓦時,同比增長約1700億千瓦時;可再生能源發(fā)電量占全年發(fā)電總量比重為26.7%,同比上升0.2個百分點。
問題:2018年,我國發(fā)電總量約為( )萬億千瓦時。
A.1.87 B.3.70 C.5.84 D.7.00
【答案】D【解析】根據(jù)文字材料可知,2018年,我國可再生能源發(fā)電量為1.87萬億千瓦時,占全年發(fā)電量比重為26.7%,則所求為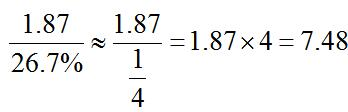 億千瓦時,結果偏大選稍小的選項,本題選擇D項。
億千瓦時,結果偏大選稍小的選項,本題選擇D項。

【例3】海州市海洋化工開發(fā)區(qū),2012年完成總產(chǎn)值為147.5億元,同比增長30.7%。
問題:2011年海州市海洋化工開發(fā)區(qū)的總產(chǎn)值是( )。
A.122.9億元 B.112.9億元 C.108.7億元 D.106.6億元
【答案】B【解析】

【例4】2007年全年地方財政支出1083.57億元,比上年增長33.4%。
問題:2007年全年地方財政支出比上年增加了( )億元。
A.269.58 B.271.30 C.362.55 D.360.44
【解析】B。由材料可知,2007年全年地方財政支出比上年增加了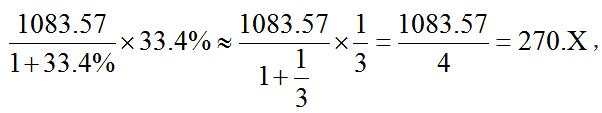 結果偏小選稍大選項,本題選擇B項。
結果偏小選稍大選項,本題選擇B項。

四、總結
對于特征數(shù)字法,重點在于熟悉其常見的應用環(huán)境以及掌握百分數(shù)轉換成分數(shù)的運用。同時,希望同學們繼續(xù)關注“政華公考”,下載“政華公考”app,學習更多的做題技巧。
行測資料分析:“藏”在兩數(shù)之比變化中的增長率
在行測資料分析中,可以寫成 形式的列式我們統(tǒng)稱為兩數(shù)之比,常考的有比重、平均數(shù)以及倍數(shù),還有收入利潤率、產(chǎn)銷率等等。當我們已知分子分母的增長率的大小關系時,就可以直接判斷現(xiàn)期兩數(shù)之比與基期兩數(shù)之比相比較的變化情況。
形式的列式我們統(tǒng)稱為兩數(shù)之比,常考的有比重、平均數(shù)以及倍數(shù),還有收入利潤率、產(chǎn)銷率等等。當我們已知分子分母的增長率的大小關系時,就可以直接判斷現(xiàn)期兩數(shù)之比與基期兩數(shù)之比相比較的變化情況。

例題:2018年全年糧食種植面積11704萬公頃,比上年減少95萬公頃,減少0.8%。全年糧食產(chǎn)量65789萬噸,比上年減少371萬噸,減產(chǎn)0.6%。
問題:2018年全年糧食平均產(chǎn)量與上年相比提高了。(判斷正誤)
【答案】正確【解析】結合材料,問題所涉及的 糧食產(chǎn)量看作A,糧食面積看作B,所以判斷兩數(shù)之比的變化,從材料中可知qa=-0.6%,qb=-0.8%,即qa>qb,現(xiàn)期比基期增加,所以2018年全年糧食平均產(chǎn)量與上年相比提高,故正確。
糧食產(chǎn)量看作A,糧食面積看作B,所以判斷兩數(shù)之比的變化,從材料中可知qa=-0.6%,qb=-0.8%,即qa>qb,現(xiàn)期比基期增加,所以2018年全年糧食平均產(chǎn)量與上年相比提高,故正確。
以上例題是該考點的基礎考查形式,但其變形考查形式,成為了考生的復習痛點,不僅錯誤率居高不下,且常常會浪費掉大量時間。
接下來,一起看看“藏”在兩數(shù)之比變化中的增長率。
例1:2018年末全國大陸總人口139538萬人,比上年末增加530萬人,其中城鎮(zhèn)常住人口83137萬人,占總人口比重(常住人口城鎮(zhèn)化率)為59.58%,比上年末提高1.06個百分點。
問題:2018年末城鎮(zhèn)常住人口增長速度比全國大陸總人口增長速度快。(判斷正誤)
【答案】正確【解析】所求為判斷城鎮(zhèn)常住人口增長速度和全國大陸總人口增長速度的大小關系,即兩個增長率比較大小,結合材料,兩個增長率并沒有直接給出,但材料中給出城鎮(zhèn)常住人口占全國大陸總人口的比重,以及比上年末提高1.06個百分點,即現(xiàn)期與基期比,比重上升,所以可以得到qa>qb,該比重中的A為城鎮(zhèn)常住人口,B為全國大陸總人口,所以城鎮(zhèn)常住人口增長速度大于全國大陸總人口增長速度,故正確。
例2:2018年全年總用水量6110億立方米,比上年增長1.1%。人均用水量439立方米,比上年增長0.6%。
問題:2018年全年我國人口增長速度低于1.1%。(判斷正誤)
【答案】正確【解析】關于問題所求的是我國人口增長速度,材料中無直接相關數(shù)據(jù),但是“人均用水量”中涉及人口指標, 是兩數(shù)之比的形式,且“比上年增長0.6%”,即現(xiàn)期與基期比,兩數(shù)之比(平均數(shù))上升,所以可以得到qa>qb。總用水量看作A,我國人口看作B,材料中已知“全年總用水量比上年增長1.1%”,即qa=1.1%,所以2018年全年我國人口增長速度(qb)小于1.1%,故正確。
是兩數(shù)之比的形式,且“比上年增長0.6%”,即現(xiàn)期與基期比,兩數(shù)之比(平均數(shù))上升,所以可以得到qa>qb。總用水量看作A,我國人口看作B,材料中已知“全年總用水量比上年增長1.1%”,即qa=1.1%,所以2018年全年我國人口增長速度(qb)小于1.1%,故正確。
通過上述題目可知,已知兩數(shù)之比的變化,反推增長率的大小關系,其本質考點與已知增長率的大小關系判斷兩數(shù)之比的變化一致,難度不大。但是隱蔽性很強,放在整套題中“藏”得很深,使考生很難發(fā)現(xiàn)。因此考生平時需要注重積累,多加練習,增強敏感性。
行測資料分析:乘除變加減——錯位加減計算增長量
題型示例

但是常規(guī)算法需要計算乘除法,計算難度較高。如何巧妙地避免計算復雜的乘除法,轉而計算較簡單的加減法呢?
通過觀察上式,我們可以發(fā)現(xiàn)在不考慮小數(shù)點的情況下近似看成 此時157和116兩個數(shù)較為接近,如果能近似地化為相同的數(shù)即可約掉,即在116的基礎上加上41。但為了保證分數(shù)值不變,則需要分子分母同時擴大相同的倍數(shù)。下面政華公考就具體來研究如何通過加減來實現(xiàn)分子分母同時擴大或縮小。
此時157和116兩個數(shù)較為接近,如果能近似地化為相同的數(shù)即可約掉,即在116的基礎上加上41。但為了保證分數(shù)值不變,則需要分子分母同時擴大相同的倍數(shù)。下面政華公考就具體來研究如何通過加減來實現(xiàn)分子分母同時擴大或縮小。
方法原理

上式中,當分母加上1234.5相當于將分母擴大為(1+10%)倍,則分子也要擴大相同的倍數(shù),則相當于在分子上加了5432.1。同理,如果分母上加123.45則分子上加543.21。
為了簡化這一操作,我們采取了保留原式的前三位有效數(shù)字的方式,如下式:
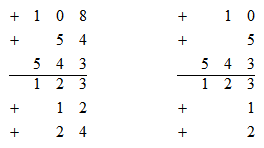
通過觀察可得到結論:當分母加上或減去首兩位的倍數(shù)時,分子也需要加上或減去其首兩位相應的倍數(shù);當分母加上或減去首一位的倍數(shù)時,分子也需要加上或減去其首一位相應的倍數(shù)。但我們常見的情況也并非剛剛好都是首兩位或者首一位的倍數(shù),如下式:
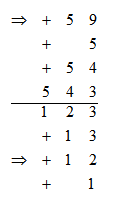
對于這種情況我們可以利用首兩位以及首一位的倍數(shù)湊出我們想要的數(shù),進而將分子作相應的變化即可。上式中,我們將分母加上的13看成先加12再加1,所以分子上對應要先加54再加5,即加59。
總結口訣:錯相同位,加減相同倍。
所以利用以上方法計算例1步驟如下:

方法應用
例題:截至2021年年底,全國60周歲以上老年人口24949萬人,占總人口的17.9%,其中享受高齡補貼的老年人2682.2萬人,比上年增長13.9%。
問題:2021年年底,我國享受高齡補貼的老年人口同比增加多少萬人?( )
A.271 B.304 C.327 D.355
【答案】C【解析】由材料可知,2021年享受高齡補貼的老年人2682.2萬人,比上年增長13.9%。所求為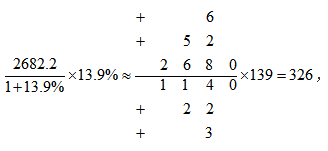 選擇最接近的C。
選擇最接近的C。
通過以上講解,對于 類型的計算,我們就可以利用上述錯位加減的方法估算。在日常備考過程中也需要大家多加練習,才能真正地將這個算法運用自如。
類型的計算,我們就可以利用上述錯位加減的方法估算。在日常備考過程中也需要大家多加練習,才能真正地將這個算法運用自如。








