行測(cè)數(shù)量關(guān)系快速解題技巧
整除幫你快速解題
關(guān)于行測(cè)數(shù)量關(guān)系題，只要用對(duì)方法是可以快速選出正確選項(xiàng)的，其中有一種方法就是利用整除的思維，所以，今天帶領(lǐng)大家了解并掌握如何利用整除快速解題。
一、整除的概念
若a÷b=c(a、b、c均為整數(shù))，則a能被b整除。
二、整除關(guān)系的確定
在做題過(guò)程中，大部分題目涉及的數(shù)據(jù)都是整數(shù)，這個(gè)時(shí)候就可以考慮用整除解題了。什么時(shí)候確定可以用整除呢？這就需要我們對(duì)一些關(guān)鍵信息敏感一些。
1、文字描述：題干中出現(xiàn)“整除、平均、每、倍”等字眼時(shí)，一般存在整除關(guān)系。
例1：某班級(jí)發(fā)放課外書，平均每人能分到7本。后來(lái)該班級(jí)又轉(zhuǎn)來(lái)若干學(xué)生，這樣每人能分到6本，該班級(jí)課外書總數(shù)是（ ）。
A.180本 B.210本 C.240本 D.280本
【答案】B【解析】題干中出現(xiàn)了“平均每”這樣的字眼，考慮用整除。由題意可知，課外書總數(shù)=7×班級(jí)原人數(shù)=6×班級(jí)現(xiàn)人數(shù)，則課外書總數(shù)能被7和6整除，選項(xiàng)中只有B符合。
2、特征數(shù)據(jù)：題干出現(xiàn)“分?jǐn)?shù)、百分?jǐn)?shù)、比例”等特征數(shù)據(jù)時(shí)一般也存在整除關(guān)系。
例2：學(xué)校有足球和籃球的數(shù)量比為8∶7，先買進(jìn)若干個(gè)足球，這時(shí)足球與籃球的比變?yōu)?∶2，接著又買進(jìn)一些籃球，這時(shí)足球與籃球數(shù)量比變?yōu)?∶6，已知買進(jìn)的籃球比買進(jìn)的足球多3個(gè)，原來(lái)足球有多少個(gè)（ ）？
A.48 B.42 C.36 D.30
【答案】A【解析】題干中出現(xiàn)了比例，考慮用整除。題目求的是原來(lái)的足球有多少個(gè)，在題干中，已知學(xué)校原有足球和籃球的數(shù)量比是8∶7，可以確定原來(lái)的足球數(shù)量能被8整除，排除B、C、D，只有A符合條件。
三、學(xué)以致用
相信同學(xué)們對(duì)整除的概念和用法都有所了解了，接下來(lái)再來(lái)看一道題目，大家可以嘗試用不同的方法解題，通過(guò)對(duì)比進(jìn)一步感知整除的快捷。
例3：若干學(xué)生住若干房間，如果每間住4人，則有20人沒(méi)地方住，如果每間住8人，則有一間房只有4人住，問(wèn)共有多少學(xué)生？
A.30 B.34 C.40 D.44
【答案】D【解析】方法一：根據(jù)題干可知，兩種安排方案中學(xué)生人數(shù)是不變的，可圍繞著學(xué)生人數(shù)構(gòu)造等量關(guān)系。設(shè)房間數(shù)為x，得到4x+20=8(x-1)+4，求得x=6，進(jìn)而得到學(xué)生人數(shù)為4×6+20=44人，選D。
方法二：題干中出現(xiàn)“每”字眼，考慮用整除。根據(jù)每間住4人，則有20人沒(méi)地方住可知，學(xué)生人數(shù)減20能被4整除，20能被4整除，即人數(shù)能被4整除。排除A、B選項(xiàng)。根據(jù)每間住8人，則有一間房只有4人住可知，學(xué)生人數(shù)減4能被8整除，只有D符合條件。
通過(guò)不同解題方法的對(duì)比，整除的方法是不是更加方便快捷？同學(xué)們快點(diǎn)運(yùn)用起來(lái)吧。
淺談行測(cè)數(shù)量關(guān)系中的比較構(gòu)造法
在公務(wù)員考試中，行測(cè)中的數(shù)量關(guān)系的題型是大家比較頭痛的，也是大家比較想放棄的，我們要做到的是在考試中盡可能快速地選擇幾道數(shù)量關(guān)系的題目來(lái)做。選擇什么樣的題目就尤為重要了，同樣在快速求解的時(shí)候利用什么方法也很重要，下面給大家講解數(shù)量關(guān)系中常見(jiàn)的應(yīng)用方法——比較構(gòu)造法。
一、含義
比較構(gòu)造法指的是對(duì)同一件事有兩種或兩種以上完成方案，通過(guò)比較方案間的差異，從而構(gòu)造等量關(guān)系求解的方法。我們一起來(lái)看個(gè)例子。
例1：某車隊(duì)運(yùn)輸一批蔬菜。如果每輛汽車運(yùn)3500千克，那么還剩下5000千克；如果每輛汽車運(yùn)4000千克，那么還剩下500千克，則該車隊(duì)有（ ）輛汽車。
A.8 B.9 C.10 D.11
【答案】B【解析】根據(jù)題意，有兩種運(yùn)輸方案，可對(duì)比兩種方案的差異進(jìn)行求解。
對(duì)比兩種方案可知，每輛車要是多運(yùn)輸500千克，總共能多運(yùn)輸4500千克，所以共有(5000-500)÷(4000-3500)=9輛車。由選項(xiàng)可知，本題選擇B項(xiàng)。
二、比較構(gòu)造法的應(yīng)用
例2：有一批汽車零件由A和B負(fù)責(zé)加工，A每天比B少做3個(gè)零件。如果A和B兩人合作需要18天才能完成，現(xiàn)在讓A先做12天，然后B再做17天，還剩這批零件的1/6沒(méi)有完成，這批零件共有多少個(gè)？（ ）
A.240 B.250 C.270 D.300
【答案】C【解析】已知A和B合作需要18天才能完成，那么A和B合作完成5/6的零件需要18×5/6=15天。若以完成5/6工作量的時(shí)間進(jìn)行分析可得：
A做3天的工作量=B做2天的工作量，所以PA：PB=2：3，已知A每天比B少做3個(gè)零件，所以一份等于3，可得A和B每天共做(2+3)×3=15個(gè)零件。所以這批零件共有15×18=270個(gè)。由選項(xiàng)可知，本題選擇C項(xiàng)。
通過(guò)上述題目希望大家對(duì)于比較構(gòu)造法有一定的了解與認(rèn)識(shí)，所謂比較構(gòu)造就是我們要對(duì)比方案間的差異，來(lái)構(gòu)建等量關(guān)系求解。同時(shí)依然需要大家在以后的備考中能夠應(yīng)用到相應(yīng)的題目中，提高解題速度。
正反比——行測(cè)數(shù)學(xué)運(yùn)算解題小妙招
工程、行程問(wèn)題作為行測(cè)考試中的常見(jiàn)題型，除了可以應(yīng)用方程法求解，還有一種比較簡(jiǎn)便的方法——正反比。正反比相對(duì)于常見(jiàn)的方程求解，其最大的優(yōu)勢(shì)在于簡(jiǎn)化計(jì)算量，降低了計(jì)算難度，可以很大程度上幫助我們快速得出答案。在此進(jìn)行展開(kāi)分析。
一、正反比的應(yīng)用環(huán)境
在行程問(wèn)題中，路程=速度×?xí)r間；工程問(wèn)題中，工作總量=工作效率×?xí)r間，兩者的公式本質(zhì)上都是M=A×B的形式。當(dāng)A為定值，M與B成正比關(guān)系；B為定值，M與A成正比關(guān)系；當(dāng)M為定值，A與B成反比關(guān)系。所以，只要在M=A×B的模型中，滿足三個(gè)量中某一個(gè)量為定值，就可以用正反比關(guān)系來(lái)解題了。
二、正反比的應(yīng)用
例1：一架戰(zhàn)斗機(jī)從甲機(jī)場(chǎng)勻速開(kāi)往乙機(jī)場(chǎng)，如果速度提高25%，可比原定時(shí)間提前12分鐘到達(dá)；如果以原定速度飛行600千米后，再將速度提高1/3，可以提前5分鐘到達(dá)。那么甲、乙兩機(jī)場(chǎng)的距離是多少千米？（ ）
A.750 B.800 C.900 D.1000
【答案】C【解析】方法一，利用方程求解，設(shè)原速為v千米/小時(shí)，原定時(shí)間為t小時(shí)，則根據(jù)路程一定可得，v×t=(1+25%)v×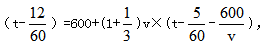
解得t=1，v=900，則總路程為900×1=900千米。
方法二，路程一定，利用正反比求解，速度提高25%后，速度之比為4：5，原定時(shí)間與所需時(shí)間的比為5：4，差1份，對(duì)應(yīng)12分鐘，則原定時(shí)間為12×5=60分鐘。飛行600千米后的剩余路程，速度之比為3：4，原定時(shí)間與所需時(shí)間的比為4：3，，差1份，對(duì)應(yīng)5分鐘，則剩余路程的原定時(shí)間為4×5=20分鐘，故飛行600千米所用時(shí)間為60-20=40分鐘，則甲、乙兩機(jī)場(chǎng)的距離為600÷40×60=900千米。
例2：某工廠計(jì)劃在一定時(shí)間內(nèi)生產(chǎn)一批計(jì)算機(jī)，如果每天生產(chǎn)140臺(tái)，可提前3天完成，如果每天生產(chǎn)120臺(tái)，則要再生產(chǎn)3天才能完成，問(wèn)規(guī)定完成的時(shí)間是多少天？（ ）
A.30 B.33 C.36 D.39
【答案】D【解析】方法一，利用方程求解，兩者方式工作總量不變，設(shè)規(guī)定完成的時(shí)間為t天。總量=140×(t-3)=120×(t+3)，解得t=39。
方法二，利用正反比求解，計(jì)算機(jī)的總量不變，效率的比值為140：120=7：6，則時(shí)間的比值為6：7，時(shí)間的比例上相差一份，具體時(shí)間相差6天，1份對(duì)應(yīng)6天，則按照140臺(tái)的效率去算，6份對(duì)應(yīng)36天，提前3天完成，因此原計(jì)劃39天，選擇D。
通多對(duì)比以上兩道題目的不同解題方式可以發(fā)現(xiàn)，方程法列式更為直觀，但解題的計(jì)算量比較大，而正反比的方法更側(cè)重于思維方式的轉(zhuǎn)變，計(jì)算難度較低，可以極大地節(jié)省時(shí)間。
行測(cè)數(shù)量關(guān)系：找到“最不利”，方可無(wú)往而不利
成功學(xué)理論告訴我們，一個(gè)人如果想要成功，必得經(jīng)受最不利的形勢(shì)，才能觸底反彈，收獲成功，對(duì)于這個(gè)成功學(xué)的邏輯，不僅適用于工作，也適合解決行測(cè)數(shù)量關(guān)系中的一類問(wèn)題，這類問(wèn)題需要找到最不利情況后再求解。具體來(lái)看看下邊的題目。
例題：一個(gè)暗箱中有同樣大小，同樣質(zhì)地的黑球和白球各5個(gè)。問(wèn)至少?gòu)南渥又心贸龆嗌賯€(gè)球才能保證拿到白球？
【解析】此題問(wèn)法中有兩個(gè)要求，一是最少，二是保證。要保證拿到白球，就需要考慮最不利情況，也就是與拿到白球一線之差的情況，成功就是拿到白球，對(duì)于此題，最不利的情況就是將黑球全都拿出來(lái)，此時(shí)再拿1個(gè)球，拿出的一定是白球，即保證拿到白球，且滿足題干要求的最少。因此，至少需要拿出5+1=6個(gè)球才能保證拿到白球。
【點(diǎn)撥】
此類題目的題型特征為題干中出現(xiàn)“至少……才能保證(就一定)”的表述；
解題原則為最不利原則，在取的過(guò)程中盡量先讓結(jié)果不發(fā)生，即與成功一線之差。
結(jié)果的計(jì)算為最不利情況數(shù)加1。
接下來(lái)通過(guò)例題來(lái)感受下如何使用最不利原則求解題。
例1：某高校舉辦的一次讀書會(huì)共有38位學(xué)生報(bào)名參加，其中中文、歷史、哲學(xué)專業(yè)各有10位學(xué)生報(bào)名參加了此次讀書會(huì)，另外還有4位化學(xué)專業(yè)學(xué)生和4位物理專業(yè)的學(xué)生也報(bào)名參加了此次讀書會(huì)，那么一次至少選出（ ）位學(xué)生，將能保證選出的學(xué)生中至少有5位學(xué)生是同一專業(yè)的。
A.17 B.20 C.21 D.39
【答案】C【解析】題目問(wèn)“至少……才能保證”，符合最不利原則解決的問(wèn)題特征。利用最不利原則可知，“至少有5位學(xué)生是同一專業(yè)”的最不利的情況是“4位同學(xué)是同一專業(yè)”，先選出中文、歷史、哲學(xué)、物理以及化學(xué)專業(yè)的學(xué)生各4位，此時(shí)若再選出1位學(xué)生就可以保證至少有5位學(xué)生是同一專業(yè)的，因此共選出4×5+1=21位，選擇C項(xiàng)。
例2：有四種顏色的文件夾若干，每人可取1-2個(gè)，至少有幾人去取，才能保證有3人所取到的文件夾完全相同？（ ）
A.20 B.21 C.28 D.29
【答案】D【解析】由題可知，題目問(wèn)“至少……才能保證”，符合最不利原則解決的問(wèn)題特征。根據(jù)題意可知，取1個(gè)文件夾時(shí)，則有4種情況；取2個(gè)文件夾時(shí)，如果兩個(gè)文件夾顏色相同，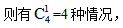
如果兩個(gè)文件夾顏色不同，
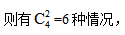因此取出的文件夾共有4+4+6=14種情況。利用最不利原則可知，“3人取到的文件夾完全相同”的最不利情況是“每種文件情況都有2人取到”，那么此時(shí)再來(lái)1個(gè)人，就一定保證有3人取得的文件夾情況完全相同，因此至少要有14×2+1=29個(gè)人，選擇D項(xiàng)。
【點(diǎn)撥】當(dāng)最不利情況數(shù)不明確時(shí)，需要結(jié)合排列組合求出所有情況總數(shù)，再利用最不利情況數(shù)+1求解。
不管是人生還是做題，必先經(jīng)歷最不利的情況，才能觸底反彈，逆風(fēng)飛翔，方可擁有“無(wú)往而不利”的模樣。所以，小伙伴們，為了那副“驕傲的模樣”，趕緊刷題再走一趟。
