行測數(shù)量關(guān)系：工程問題
工程問題概述
（一）核心公式
工作總量=工作效率×工作時(shí)間
注：
①當(dāng)工作效率一定的情況下，工作總量與工作時(shí)間呈正比例；
②當(dāng)工作時(shí)間一定的情況下，工作總量與工作效率呈正比例；
③當(dāng)工作總量一定的情況下，工作時(shí)間與工作效率呈反比例。
（二）高頻考法題干特征
1.給定時(shí)間型：題目中只給定不同主體的完工時(shí)間，其余量未知。
2.效率制約型：題目中不僅給定工作時(shí)間，還給出效率的比例倍數(shù)關(guān)系。
（三）解題思路：賦值法
1.給完工時(shí)間
①賦總量（完工時(shí)間的公倍數(shù)）
②算效率：效率=總量÷時(shí)間
③根據(jù)工作過程列方程
完工時(shí)間：一次性完成全部工作所需的時(shí)間
2.給效率比例
①賦效率（滿足比例即可）
②算總量：效率×?xí)r間=總量
③根據(jù)工作過程列方程
3.條件綜合型
這一類區(qū)別于前兩個(gè)題型，題目中關(guān)于工程問題公式的三個(gè)量給了兩個(gè)或兩個(gè)以上的時(shí)候，條件較多的工程問題，那么就利用工作總量不變列方程解答即可。
例題1：為支持“一帶一路”建設(shè)，某公司派出甲、乙兩隊(duì)工程人員出國參與一個(gè)高鐵建設(shè)項(xiàng)目。如果由甲隊(duì)單獨(dú)施工，200天可完成該項(xiàng)目；如果由乙隊(duì)單獨(dú)施工，則需要300天。甲、乙兩隊(duì)共同施工60天后，甲隊(duì)被臨時(shí)調(diào)離，由乙隊(duì)單獨(dú)完成剩余任務(wù)，則完成該項(xiàng)目共需（ ）天。
A.120 B.150 C.180 D.210
【答案】D【解析】第一步，本題考查工程問題，屬于時(shí)間類。
第二步，賦值工作總量為時(shí)間（200天、300天）的公倍數(shù)600，則甲的效率是600÷200=3，乙的效率是600÷300=2。
第三步，甲、乙兩隊(duì)共同施工60天后，還剩余工作量為600-（2+3）×60=300。則乙隊(duì)單獨(dú)完成需要300÷2=150（天），完成該項(xiàng)目共需60+150=210（天）。
故正確答案為D。
例題2：A、B、C三個(gè)工程隊(duì)負(fù)責(zé)甲、乙兩段工程相同性質(zhì)的施工，現(xiàn)在先安排3個(gè)隊(duì)伍進(jìn)行5天甲段工程施工后，調(diào)A隊(duì)伍去做乙段工程，8天后恰好同時(shí)完成，已知3個(gè)工程隊(duì)效率之比為5：3：4，如果先安排3個(gè)隊(duì)伍先做甲段，中間調(diào)C隊(duì)去做乙段，也能同時(shí)完成，則C隊(duì)是在工程開始后第（ ）天開始乙段工程。
A.2 B.3 C.4 D.5
【答案】C【解析】第一步，賦ABC三個(gè)隊(duì)的效率分別為5.3.4。
第二步，求總量，甲乙兩段工程性質(zhì)相同，根據(jù)“先安排3個(gè)隊(duì)伍進(jìn)行5天甲段工程施工后，調(diào)A隊(duì)伍去做乙段工程，8天后恰好同時(shí)完成”可以算出甲工作總量為（5+3+4）×5+（3+4）×8=116，乙的工作總量為5×8=40。
第三步分析求解，調(diào)C隊(duì)去做乙，共需要40÷4=10天，即C隊(duì)被調(diào)走后10天完成甲工程，則之前做了116-（5+3）×10=36，這36的工作量是三個(gè)人一起做的，共36÷（5+3+4）=3天，故第四天開始乙段工程。
故正確答案為C。
例題3：某工程隊(duì)計(jì)劃每天修路560米，恰好可按期完成任務(wù)。如每天比計(jì)劃多修80米，則可以提前2天完成，且最后1天只需修320米。問如果要提前6天完成，每天要比計(jì)劃多修多少米？（ ）
A.160 B.240 C.320 D.400
【答案】B【解析】第一步，本題考查工程問題。
第二步，設(shè)原計(jì)劃修路時(shí)間為t天，可列方程：560t=（560+80）×（t-3）+320，解得t=20，可得修路總長度為560×20=11200（米）。
第三步，要想時(shí)間提前6天完成，即20-6=14（天）完成，則每天共需修路11200÷14=800（米），那么比原計(jì)劃每天多修800-560=240（米）。故正確答案為B。
行測工程問題解題技巧：交替合作“3+1”
對于工程問題而言，在實(shí)際考試過程中除多者合作外，還會(huì)考查交替合作題型。今天和大家來學(xué)習(xí)交替合作題型的解題方法。
交替合作含義
一般指多個(gè)主體一起合作完成一項(xiàng)工作，合作的過程中主體按照一定規(guī)律進(jìn)行輪流完成工作。例如：甲工作1小時(shí)，乙工作1小時(shí)，丙工作1小時(shí)……如此重復(fù)下去。在工作的過程中甲、乙是按照每人1小時(shí)的工作方式輪流或者合作完工的，因此稱之為是交替合作。
解題思路
1.求出工程總量和各個(gè)元素的效率。
2.找到最小循環(huán)周期，并且求出一個(gè)周期工作效率之和。
3.工作總量/一個(gè)循環(huán)周期的效率和=周期數(shù)……剩余工作量。
4.分配剩余工作總量——求出完工時(shí)間。
實(shí)戰(zhàn)練題
例1：完成某片果園的采摘工作，甲單獨(dú)完成需要18天，乙單獨(dú)完成需要24天，現(xiàn)按照甲、乙、甲、乙、……的順序輪流采摘，每人1天，那么完成這項(xiàng)工作需要多長時(shí)間？（ ）
A.19.5 B.20 C.20.5 D21
例2：某項(xiàng)工程，甲、乙、丙三個(gè)工程隊(duì)如單獨(dú)施工，分別需要12小時(shí)、10小時(shí)和8小時(shí)完成。現(xiàn)按“甲—乙—丙—甲……”的順序讓三個(gè)工程隊(duì)輪班，每隊(duì)施工1小時(shí)后換班，問該工程完成時(shí)，甲工程隊(duì)的施工時(shí)間共計(jì)：（ ）
A.2小時(shí)54分 B.3小時(shí) C.3小時(shí)54分 D.4小時(shí)
總結(jié)：工程問題作為行測常考題目類型之一，特點(diǎn)相對明顯，題目難度較小，大家只要熟悉各種題目的特點(diǎn)，明確題目的考點(diǎn)，牢記可設(shè)特值求解的情況以及解題的步驟，就能在考試的時(shí)候如魚得水。
行測作答技巧：工程問題和行程問題中的正反比
在行測數(shù)量關(guān)系的學(xué)習(xí)備考過程中，很多考生都直呼有難度、沒思路，持有一種放棄的心態(tài)。其實(shí)不然，比如今天要帶大家學(xué)習(xí)除了用最基本的方程法解答工程和行程類問題，我們還可以用快、準(zhǔn)、狠的正反比解法。其題型明確，解法清晰，可適當(dāng)減輕大家做這類題目的負(fù)擔(dān)。
一、知識(shí)精講
在一個(gè)M=A×B的關(guān)系式當(dāng)中，如果存在一個(gè)定值，則另外兩個(gè)概念有正反比關(guān)系存在。
1.當(dāng)M一定，A與B成反比；
2.當(dāng)A一定，M與B成正比；
3.當(dāng)B一定，M與A成正比。
二、工程問題中的正反比
由工作總量=效率×?xí)r間可知，當(dāng)工作總量一定，效率與時(shí)間成反比；當(dāng)效率一定，工作總量與時(shí)間成正比；當(dāng)時(shí)間一定，工作總量與效率成正比。
例題：甲工程隊(duì)計(jì)劃150天完成A這項(xiàng)工程，按照這樣的效率工作30天后，由于新工友的加入，效率提高了20%，則該項(xiàng)工程可以提前多少天完成？（ ）
A.20 B.25 C.30 D.45
【答案】A【解析】新工友加入后，效率提高20%，原效率與現(xiàn)效率之比為1：1.2=5：6，由于剩余的工作總量一定，那么時(shí)間與效率成反比，原時(shí)間與現(xiàn)時(shí)間之比為6：5，那么原時(shí)間6份對應(yīng)150-30=120天，即1份=20天，而現(xiàn)在比原來少用1份時(shí)間，那么該項(xiàng)工程可提前20天完工，故此題選A。
三、行程問題中的正反比
由路程=速度×?xí)r間可知，當(dāng)路程一定，速度與時(shí)間成反比；當(dāng)速度一定，路程與時(shí)間成正比；當(dāng)時(shí)間一定，路程與速度成正比。
例題：郵遞員騎自行車從郵局到漁村送郵件，平時(shí)需要1個(gè)小時(shí)。某天，在距離漁村2公里處，自行車出現(xiàn)故障，改成步行。已知步行速度為自行車車速的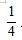
，結(jié)果比平時(shí)多用22.5分鐘。問郵局到漁村的距離是多少公里？（ ）
A.15 B.16 C.18 D.20
【答案】B【解析】由題意可知，步行速度與自行車速度之比為1：4，故障地與漁村的距離一定，為2公里，那么速度與時(shí)間成反比，即步行時(shí)間與自行車時(shí)間之比為4：1，所以步行時(shí)間比自行車時(shí)間多用三份，其對應(yīng)22.5分鐘，即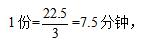
即自行車騎行兩公里的時(shí)間為7.5分鐘，所以騎行1小時(shí)（60分鐘）的距離為
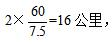即郵局到漁村的距離為16公里，故此題選B。
通過以上題目的總結(jié)發(fā)現(xiàn)，解決工程和行程類問題，我們只需要找到三個(gè)量中的不變量，再根據(jù)另外兩個(gè)量中的已知量之間的比值，推知另一個(gè)量的比值關(guān)系，找到實(shí)際值與比例的對應(yīng)關(guān)系，進(jìn)而根據(jù)題干要求尋找到答案。
吃透這一點(diǎn)，行測工程問題不再難
工程問題研究的是在實(shí)際生活生產(chǎn)中，工作總量、工作效率和工作時(shí)間三者之間關(guān)系的一類問題，屬于行測數(shù)量關(guān)系考試當(dāng)中的高頻考點(diǎn)。認(rèn)為，工程問題的解題關(guān)鍵是梳理清楚題干描述的完工方式，再結(jié)合基本公式（工作總量=工作效率×工作時(shí)間）建立等量關(guān)系，工程問題就迎刃而解。
示例
生產(chǎn)一批零件，甲車間每天生產(chǎn)100個(gè)，乙車間每天生產(chǎn)50個(gè)。若兩車間合作，8天可以完成。
（1）若甲車間先生產(chǎn)3天后，乙車間加入生產(chǎn)，則共用多少天完成？
（2）若兩車間合作，但期間甲休息了3天，乙休息若干天，最終共用12天完成任務(wù)。已知每天都有車間進(jìn)行生產(chǎn)，則乙車間休息了多少天？
【解析】
（1）根據(jù)“若兩車間合作，8天可以完成”可得工作總量為：（100+50）×8=1200個(gè)。
梳理另一種完工方式：根據(jù)“甲車間先生產(chǎn)3天后，乙車間加入生產(chǎn)”可知第一階段是甲獨(dú)自工作，工作時(shí)間為3天；第二階段甲和乙合作，設(shè)工作時(shí)間t天；根據(jù)實(shí)際完成的工作總量為1200個(gè)，可列方程：100×3+（100+50）×t=1200，解得t=6，所以共用：3+6=9（天）。
（2）本題的工作總量還是1200個(gè)，而另一種完工方式如果按階段梳理，明顯是不可行的，題干并沒有明確告訴我們每個(gè)階段是如何工作的，我們可以利用分主體的思維去梳理。根據(jù)“兩車間合作，但期間甲休息了3天，乙休息若干天，最終共用12天完成任務(wù)”可知主體甲休息3天，工作12-3=9天；設(shè)主體乙休息t天，則乙工作（12-t）天。根據(jù)實(shí)際完成工作總量為1200個(gè)，可列方程：100×9+50×（12-t）=1200，解得t=6天。
綜上，我們不難發(fā)現(xiàn)解決這類工程問題的密鑰就是梳理完工方式，而近年來經(jīng)常考察的兩種完工方式就是分階段完工和分主體完工，吃透這一點(diǎn)，工程問題不再難。
例1：甲乙兩隊(duì)完成一項(xiàng)工程的效率比為2∶5。該項(xiàng)工程，若由甲隊(duì)先單獨(dú)做3天，再由乙隊(duì)單獨(dú)做4天，最后由甲、乙兩隊(duì)合作6天剛好完成。問若由甲隊(duì)單獨(dú)完成，需要多少天？（ ）
A.32 B.33 C.34 D.35
【答案】C【解析】設(shè)甲乙兩隊(duì)的效率分別為2x和5x，設(shè)若由甲隊(duì)單獨(dú)完成，需要t天，根據(jù)題干可知完工方式：第一階段甲獨(dú)自工作3天，第二階段乙獨(dú)自工作4天，第三階段甲和乙合作工作6天，進(jìn)而可得：2x×3+5x×4+（2x+5x）×6=2xt，解得t=34。
例2：A工程隊(duì)的效率是B工程隊(duì)的2倍，某工程交給兩隊(duì)共同完成需要6天。如果兩隊(duì)的工作效率均提高一倍，且B隊(duì)中途休息了1天，問要保證工程按原來的時(shí)間完成，A隊(duì)中途最多可以休息幾天？（ ）
A.4 B.3 C.2 D.1
【答案】A【解析】設(shè)B隊(duì)的效率為x，則A隊(duì)的效率為2x，根據(jù)“工程交給兩隊(duì)共同完成需要6天”可知工作總量為（2x+x）×6=18x。根據(jù)“如果兩隊(duì)的工作效率均提高一倍，且B隊(duì)中途休息了1天，問要保證工程按原來的時(shí)間完成”可知另一種完工方式：主體A隊(duì)休息t天，工作（6-t）；主體B隊(duì)休息1天，工作5天。雖然兩種完工方式不同，但完成的工作總量相等，可得：4x×（6-t）+2x×5=18x，解得：t=4。
隨著近幾年行測題目靈活性的增強(qiáng)，工程問題的題干也變得比較難理解，但只要梳理清楚完工方式，這類題型將不再困擾你。建議各位考生多找一些工程問題練習(xí)總結(jié)，以熟練掌握。
