
行測數量關系:如何快速掌握和定最值問題
巧解和定最值問題
在行測考試當中,數量關系往往是最容易被同學們放棄的部分,有些同學一看到數量的題目下意識的就想放棄,其實這種想法是不可取的,數量的題目當中也存在一些易得分的題型,就比如說和定最值問題,今天就來說一說如何解決這類問題。
一、題型特征
已知多個數的和一定,求其中某數最值的問題。
二、解題原則及方法
求某個量的最大值,其他量應盡可能小。
求某個量的最小值,其他量應盡可能大。
三、習題練習
例題1:一次數學考試滿分為100分,某班前六名同學的平均分為95分,排名第六的同學得86分,假如每個人得分是互不相同的整數,那么排名第三的同學最少得多少分( )?
A.94 B.97 C.95 D.96
【答案】D【解析】要使排名第三的同學得分最少,則應使其他同學得分盡量多,前兩名同學最多分別得100分和99分。設排名第三的同學最少得x分,則排名第四、五名的同學最多分別得x-1,x-2分,有100+99+x+(x-1)+(x-2)+86=95×6,解得x=96,故排名第三的同學最少得96分。
規(guī)律總結:根據解題原則確定不了具體量的值,可以設未知數列方程求解。
例題2:六一兒童節(jié)期間,100名幼兒園學生參加5項活動,參加人數最多的活動人數不超過參加人數最少活動人數的2倍,則參加人數最少的活動最少有多少人參加( )?
A.10 B.11 C.12 D.13
【答案】C【解析】設參加人數最少的活動有x人,則參加人數最多的活動人數為2x人,要想參加人數最少的活動人數最少,則參加其他項目的人要盡可能多,那么參加其他三項活動的人數也可均為2x,則有2x×4+x=100,解得x=11.X,向上取整可得x=12,故參加人數最少的活動最少有12人參加。
規(guī)律總結:根據方程求解時,求出的數不是整數,問最小(至少),向上取整。
例題3:植樹節(jié)來臨之際,120人參加義務植樹活動,共分成人數不等且每組不少于10人的六個小組,每人只能參加一個小組,則參加人數第二多的小組最多有( )人。
A.32 B.34 C.36 D.38
【答案】C【解析】和一定,要使第二多的小組的人數盡量多,則其他小組的人數應盡可能少,設參加人數第二多的小組有x人,如下:

則有(x+1)+x+13+12+11+10=120,解得x=36.5,因所求為整數,且為最多,故向下取整,即參加人數第二多的小組的人數最多有36人。
規(guī)律總結:根據方程求解時,求出的數不是整數,問最多(最大),向下取整。
通過以上幾道題目,相信同學們已經對和定最值問題有了一定的了解,希望大家可以快速的掌握這種題型的解題方法,讓這類題目不再成為我們學習路上的阻礙。
行測和定最值問題之三步解題
首先,我們得知道怎樣的題型是屬于和定最值問題!和定最值,此類題型的特點就是一組數的和是一個定值,要我們求其中某個量的最大(小)值。例如,一個班上6名同學的總分和為490分,問最高分同學得分最低得幾分?這就是一種典型的和定最值問題,對于這種題目,我們只需要進行下列三個步驟即可快速求解:
1.對未知數由大到小排序:一、二、三……
2.標箭頭:↓↑(求某個量最大(小),則其余量盡可能小(大))
3.設所求為x,結合條件把其它量表示出來,再根據和一定構建等量求解。
例1:5人參加百分制考試,成績總和為330分,已知5人都及格了,成績均為整數且依據成績排名無并列名次,求第一名最少得了多少分( )?
A.67 B.68 C.69 D.70
【答案】B【解析】5個得分為5個數,和一定,求第一名的得分最小值,典型和定最值問題,直接三步走:
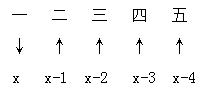
第一步:寫一~五,由大到小排序;第二步:“一”要最小,標個“↓”,那么在和一定的情況下,其他量都要大,標“↑”;第三步:設“一”為x,由于“一”求最小“二”盡可能大,兩個數需要盡可能接近且均為整數,故差1滿足,依次類推得到其余數的取值。根據得分總和為330構建等量關系:5x-10=330,解的:x=68,答案選B。
例2:植樹節(jié)來臨之際,120人參加義務植樹活動,共分成人數不等每組不少于10人的六個小組,每人只能參加一個小組,則參加人數第二多的小組最多有多少人( )?
A.32 B.34 C.36 D.38
【答案】C【解析】6個小組的人數為6個數,他們和為120,是個定值,和定最值問題,直接三步走:
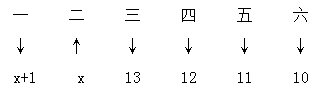
由大到小排序后,“二”要大,其余要小,標相應的箭頭;設“二”為x,那么“一”要小但又不相等,所以為x+1,又“三、四、五、六”依次要小,且最小不少于10,又互不相等,所以依次為13、12、11、10,根據6個數的和構建等量關系:2x+47=120,解得:x=36.5,求出來的x為最大值,也就是說x≤36.5,同時又是整數,故所求為36,答案選C。
此類方法其實就是準確按照三個步驟去解題即可。接下來在備考過程中勤加練習,準確判斷題目是否符合和定最值的題型,進而用此方法快速解決問題。
兩招解決和定最值問題
由于行測數學運算涉及的知識點較多,一直以來是各位考生比較頭痛的部分,尤其是遇到考查極限思維的極值類問題,大部分考生選擇直接放棄做這類題目。其實極值類問題中有一種題型相對簡單,只要掌握一定的解題技巧就可以輕松應對的和定最值問題。
【題干特征】
若干個量的加和是定值,且求某量的最大值或者最小值。
示例:兩個正整數的和為15,求①最大的數最大是多少?②最大的數最小是多少?
解析:①要求最大的數最大,另一個數要盡可能小,最小為1,最大的數最大為14;②要求最大的數最小,另一個數要盡可能大,再大也不能比最大的數大,最大為7,故最大的數最小為8。
【解題原則】
1.和一定時,求某量的最大值,讓其他量都盡量小。
2.和一定時,求某量的最小值,讓其他量都盡量大。
【刷題鞏固】
【例1】七個小朋友共采摘草莓43顆,且每人采摘的數量互不相等,采摘草莓數量最多的小朋友最多采摘了( )顆。
A.20 B.21 C.22 D.23
【答案】C【解析】七個小朋友采摘的草莓數量和一定,要使數量最多的小朋友采摘的草莓數量最多,應讓其他小朋友采摘的盡量少,又由于每個小朋友采摘數量互不相等,故其他六個小朋友采摘的數量從小到大依次是1、2、3、4、5、6,則數量最多的小朋友最多采摘43-6-5-4-3-2-1=22顆,故選C。
【例2】五人的體重之和是423斤,他們的體重都是整數,并且各不相同,則體重最輕的人最重可能為( )。
A.80斤 B.82斤 C.84斤 D.86斤
【答案】B【解析】五人的體重之和是423斤,想求體重最輕的最重,則需要其他人的體重盡可能輕且為各不相同的整數,若設體重最輕的人最重x斤,則其他四人體重從輕到重依次為(x+1)、(x+2)、(x+3)、(x+4)斤,根據和為423斤,列方程有x+x+1+x+2+x+3+x+4=423,解得x=82.6,體重最輕的人最重為82.6斤,不能比82.6斤再重,因此向下取整最重為82斤,故選B。
“小系數,同方向”解行測和定最值
應用前提
這類題目既然屬于和定最值問題,那么必然滿足和定最值的條件:和定、求最值。也就是題干中直接或間接給出了幾個數“和一定”的描述,讓求最大值或最小值。除此之外,還需能根據題干條件列出不確定具體系數的二元一次方程組。此時,我們只需要依據題干信息確定系數即可,具體為“小系數,同方向”。
口訣含義
小系數,即從系數較小的未知量入手;同方向,小系數與自身未知量取值方向相同,大系數與小系數方向相同。
經典例題
例1:觀眾對五位歌手的歌曲進行投票,每張選票都可以選擇五首歌曲中的一首或多首,但只有選擇不超過3首歌曲的選票才是有效票。五首歌曲的得票數分別為總票數的82%、73%、69%、51%和45%,那么本次投票的有效率最高可能為:( )
A.95% B.90% C.85% D.80%
【答案】B【解析】根據題干信息,可假設本次參與投票的觀眾共100人,則這100名觀眾共投出82+73+69+51+45=320票。設有效投票的人數有x人,無效投票的人數有y人,則有x+y=100;每首歌曲可投的票數有1、2、3、4、5票,不超過3票為有效票,可得n1x+n2y=320(其中n1=1、2、3,n2=4、5),根據“小系數,同方向”可知,x前的系數較小,優(yōu)先看x前系數,要使投票有效率盡可能高,則有效投票盡可能多,即x前系數要盡可能大,那么y前的系數也要盡可能地大,此時n1=3、n2=5,則有3x+5y=320,聯(lián)立方程解得x=90,即本次投票的有效率最高為90÷100×100%=90%,選擇B。
例2:參加某部門招聘考試的共有120人,考試內容共有6道題。1至6道題分別有86人、88人、92人、76人、72人和70人答對,如果答對3道或3道題以上的人員能通過考試,那么至少有多少人能通過考試( )?
A.32 B.40 C.50 D.61
【答案】D【解析】根據題干信息,本次考試共答對86+88+92+76+72+70=484題,設本次考試通過的有x人,沒有通過的有y人,根據共120人參加考試,可得x+y=120,共答對484題,可得n1x+n2y=484(其中n1=3、4、5、6,n2=1、2),根據“小系數,同方向”可知,y前的系數較小,優(yōu)先看y前系數,要使通過考試的人最少,則未通過考試的人答對的題目盡可能多,即y前系數要盡可能大,那么x前的系數也要盡可能地大,此時n1=6、n2=2,則有6x+2y=484,聯(lián)立方程解得x=61,選擇D。
通過以上題目,我們可以看到解決這類和定最值問題,關鍵是理解“小系數,同方向”這一解題原則,大家可以多找一些此類題目練習,以便熟練地掌握此種方法。








