數(shù)量關(guān)系考點(diǎn)——排列組合
知識(shí)引導(dǎo)
排列組合題常用到以下四種解題方法：
1.優(yōu)限法
適用環(huán)境：題干中出現(xiàn)有絕對(duì)限制條件的元素或者位置時(shí)，考慮用優(yōu)限法。
具體操作：優(yōu)先安排有限制條件的元素或者位置，再安排其他元素或者位置。
【例1】一次會(huì)議某單位邀請(qǐng)了10名專(zhuān)家，該單位預(yù)定了10個(gè)房間，其中一層5間、二層5間。已知邀請(qǐng)專(zhuān)家中4人要求住二層、3人要求住一層、其余3人住任一層均可。那么要滿(mǎn)足他們的住房要求且每人1間，有多少種不同的安排方法（ ）？
A.75 B.450 C.7200 D.43200
【答案】D【解析】本題中要將10名專(zhuān)家安排到10個(gè)房間，且每間安排一人。在安排過(guò)程中提到兩個(gè)要求：1.4人要求住2層，2.3人要求住1層。這兩個(gè)要求就體現(xiàn)了我們說(shuō)的“有絕對(duì)限制條件的元素”。因此我們考慮用優(yōu)限法解決。共有10人，其中4人要求住2層，從二層的5個(gè)房間中選出4個(gè)，安排4人入住，其方法數(shù)為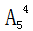
，3人要求住一層，從一層的5個(gè)房間中選出3個(gè)，安排3人入住，其方法數(shù)為
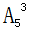，其余3人安排住剩下的3個(gè)房間，其方法數(shù)為
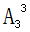，故共有
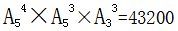種不同的安排方案。
2.捆綁法
適用環(huán)境：題干中要求元素相鄰或者位置相鄰時(shí)，考慮捆綁法。
具體操作：先考慮整體的順序要求，再考慮整體內(nèi)部的順序要求。
【例2】為加強(qiáng)機(jī)關(guān)文化建設(shè)某市直機(jī)關(guān)在系統(tǒng)內(nèi)舉辦演講比賽3個(gè)部門(mén)分別派出3、2、4名選手參加比賽，要求每個(gè)部門(mén)的參賽選手比賽順序必須相連，問(wèn)不同的參賽順序的種數(shù)在以下哪個(gè)范圍之內(nèi)（ ）？
A.小于1000 B.1000-5000 C.5001-20000 D.大于20000
【答案】B【解析】本題中要安排3個(gè)部門(mén)中參賽選手的演出順序。在安排過(guò)程中要求每個(gè)部門(mén)的參賽選手比賽順序必須相連。這個(gè)要求體現(xiàn)了我們說(shuō)的“元素相鄰”，考慮用捆綁法，首先將三個(gè)部門(mén)的選手看成3個(gè)整體，考慮三個(gè)整體的出場(chǎng)順序，有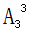
=6種；其次考慮每個(gè)整體內(nèi)選手的出場(chǎng)順序，分別有
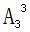=6種，
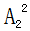=2種，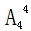
=24種。則不同參賽順序的種數(shù)為6×6×2×24=1728，計(jì)算結(jié)果顯然大于1000小于5000，故此題答案為B。
3.插空法
適用環(huán)境：題干中要求元素不相鄰時(shí)，考慮插空法。
具體操作：先安排其他元素的位置，再將不相鄰的元素插空安排。
【例3】由數(shù)字1、2、3、4、5組成無(wú)重復(fù)數(shù)字的五位數(shù)，兩個(gè)偶數(shù)互不相鄰的五位數(shù)有幾個(gè)？
【答案】72個(gè)【解析】本題中要用1-5個(gè)組成無(wú)重復(fù)數(shù)字的五位數(shù)，組數(shù)過(guò)程中要求兩個(gè)偶數(shù)互不相鄰，這體現(xiàn)了我們說(shuō)的“要求元素不相鄰”，考慮用插空法。先安排剩余的3個(gè)奇數(shù)，有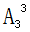
=6種，再?gòu)钠鏀?shù)形成的4個(gè)空位中選2個(gè)空將剩余的2個(gè)偶數(shù)放入，有
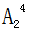=12種，因此所求為6×12=72個(gè)。
4.間接法
如果題目直接考慮需要分類(lèi)比較多，而它的對(duì)立面包含情況比較少方便計(jì)算，我們可以用總方法數(shù)減去對(duì)立面方法數(shù)進(jìn)行計(jì)算。
練習(xí)題
例1：五名優(yōu)秀組員按順序做年終總結(jié)報(bào)告，小張只能第一個(gè)或最后一個(gè)作報(bào)告，一共有多少種報(bào)告順序（ ）？
A.24 B.36 C.48 D.60
【答案】C【解析】分析題目，其中對(duì)于小張而言，有絕對(duì)的位置限制，那么這道題應(yīng)該采用優(yōu)限法來(lái)解題，要優(yōu)先考慮小張的位置。由于小張只能第一個(gè)或最后一個(gè)作報(bào)告，那他只能從這兩個(gè)位置中選一個(gè)，有2種選擇方法。對(duì)于其他人而言，題目沒(méi)有任何限制，那剩余的4人可以任意選擇報(bào)告位置，有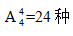
選擇方法，所以共2×24=48種報(bào)告順序，結(jié)合選項(xiàng)，答案就是C。
例2：五名優(yōu)秀組員按順序做年終總結(jié)報(bào)告，同部門(mén)的小張和小李順序相鄰，一共有多少種報(bào)告方式（ ）？
A.24 B.36 C.48 D.60
【答案】C【解析】分析題目，小張和小李相鄰作報(bào)告，所以這道題應(yīng)該采用捆綁法來(lái)解答。假設(shè)將小張與小李捆綁在一起，則小張與小李作報(bào)告順序一定相鄰。將小張和小李看作一個(gè)整體，與剩余三人進(jìn)行排序，共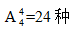
報(bào)告順序，但是小張與小李兩個(gè)人之間也要排序，共2種報(bào)告順序。所以一共有24×2=48種報(bào)告順序，所以答案選C。
例3：五名優(yōu)秀組員按順序做年終總結(jié)報(bào)告，同部門(mén)的小張和小李順序不能相鄰，一共有多少種報(bào)告順序（ ）？
A.64 B.72 C.86 D.98
【答案】B【解析】分析題目，小張和小李不相鄰，所以這道題應(yīng)該采用插空法來(lái)解答。插空法的使用原則是先將沒(méi)有要求的人的順序排好，再將小張和小李插入這些人形成的空隙中，則小張和小李自然不相鄰。根據(jù)這個(gè)方法，除小張與小李外，還有3個(gè)人，3個(gè)人排序方法有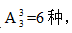
3個(gè)人形成了4個(gè)空位，再?gòu)?個(gè)空位中選兩個(gè)出來(lái)讓小明和小紅去插入，有
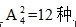順序，則總的報(bào)告順序有6×12=72種。故答案選B。
例4：某交警大隊(duì)的16名民警中，男性為10人。現(xiàn)要選4人進(jìn)行夜間巡邏工作，要求男性民警不得少于2人，問(wèn)：有多少種選人方法？
A.1605 B.1520 C.1071 D.930
【答案】A【解析】男性民警為10人，則女性民警有6人。現(xiàn)要選四人且男性民警不得少于兩人，所以采用間接法，則男民警可以有2人、3人、4人，這三類(lèi)情況，情況數(shù)較多，考慮對(duì)立面，男性民警少于2人，即沒(méi)有男性民警或只有1名男性民警，兩類(lèi)情況，所以我們可以用總的情況數(shù)-1男3女的情況數(shù)-0男4女的情況數(shù)求解，則本題所求為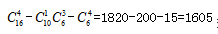
種。故本題選A。
排列組合之隔板模型
一、隔板模型的含義及基本公式
隔板模型，即將n個(gè)相同元素分給m個(gè)不同對(duì)象，要求元素全部分完，且每個(gè)對(duì)象至少分一個(gè)元素的模型，可見(jiàn)下題：
例1：現(xiàn)有7個(gè)一樣的蘋(píng)果，要分給3個(gè)小朋友，每人至少分1個(gè)，請(qǐng)問(wèn)有多少種分法？
【解析】題目要求把7個(gè)一樣的蘋(píng)果分給3個(gè)小朋友，每人至少分1個(gè)。可理解為將7個(gè)蘋(píng)果擺成一排，在中間的6個(gè)空中選2個(gè)空分別放隔板。此時(shí)將蘋(píng)果分為3堆，對(duì)應(yīng)3個(gè)小朋友分到的蘋(píng)果，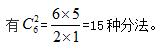
由上題，我們也可以總結(jié)出隔板模型的基本公式：將n個(gè)相同元素分給m個(gè)不同對(duì)象，要求元素全部分完，且每個(gè)對(duì)象至少分一個(gè)元素，方法數(shù)為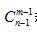
種。
二、隔板模型的靈活應(yīng)用
1.變式一：將n個(gè)相同元素分給m個(gè)不同對(duì)象，要求元素全部分完，且每個(gè)對(duì)象至少分n個(gè)元素。考慮先給每個(gè)對(duì)象分n-1個(gè)元素，再利用基本公式求解。
例2：10個(gè)蘋(píng)果分給3個(gè)人，每人至少分2個(gè)，有多少種分法？
【解析】10個(gè)蘋(píng)果分給3個(gè)人，每人至少分2個(gè)。考慮先給每人分1個(gè)蘋(píng)果，那么還剩下7個(gè)蘋(píng)果。問(wèn)題轉(zhuǎn)化為繼續(xù)將7個(gè)蘋(píng)果分給3個(gè)人，每人至少分1個(gè)。根據(jù)隔板模型基本公式，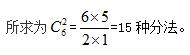
2.變式二：將n個(gè)相同元素分給m個(gè)不同對(duì)象，要求元素全部分完，任意分配。考慮先從每個(gè)對(duì)象分別借一個(gè)元素，再利用基本公式求解。
例3：某幼兒園購(gòu)買(mǎi)了15瓶飲料，要分給小明、小紅、小張3名小朋友。假設(shè)這些飲料任意分配給3名小朋友，則共有多少種不同的分配方式？
【解析】15瓶飲料分給3名小朋友，每人至少分0瓶。考慮先從每名小朋友借1瓶飲料，此時(shí)共有18瓶飲料，由于要還每人1瓶，所以此題就轉(zhuǎn)換成了將18瓶飲料分給3名小朋友，每人至少分1瓶。根據(jù)隔板模型基本公式，所求為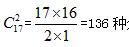
分配方式。
行測(cè)數(shù)量關(guān)系隔板“變形計(jì)”
排列組合是行測(cè)考試中難度較高的一類(lèi)題型，但是“相同元素分配給不同對(duì)象”這類(lèi)題目有固定的解題方法，那就是“隔板模型”，只要勤加學(xué)習(xí)，此類(lèi)題目求解會(huì)變得非常容易。然而在實(shí)際考試當(dāng)中，出題人總是會(huì)給同學(xué)們?cè)O(shè)置障礙，對(duì)基本模型進(jìn)行變形混淆大家做題的思路。下面就帶大家一起來(lái)了解一下隔板模型及常見(jiàn)變形題目的解答方法。
例1：將15塊相同的糖果分給3個(gè)小朋友，每人至少分1塊，有多少種分配方法（ ）？
A.89 B.90 C.91 D.92
【答案】C【解析】把15塊相同的糖果放成一排后，糖果間會(huì)形成14個(gè)空位，在這些空位中插入2個(gè)隔板就能將糖果分隔成3堆。因此小朋友們依次以堆為單位分掉糖果即可，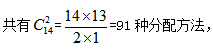
選擇C項(xiàng)。
小結(jié)1：隔板模型：將n個(gè)相同的元素分給m個(gè)不同的對(duì)象，每個(gè)對(duì)象至少分1個(gè)，分配的方法數(shù)為：
例2：將20個(gè)相同的籃球分給4個(gè)班級(jí)，每個(gè)班級(jí)至少分2個(gè)籃球，共有多少種分配方法（ ）？
A.455 B.441 C.400 D.315
【答案】A【解析】本題與例1相似，但略有不同，區(qū)別在于：例1中每個(gè)對(duì)象至少分1個(gè)，而例2中每個(gè)對(duì)象至少分2個(gè)。在分配時(shí)，可以每班先分1個(gè)，共分掉4個(gè)之后，本題就轉(zhuǎn)化成為“將16個(gè)相同的籃球分給4個(gè)班級(jí)，每個(gè)班級(jí)至少分1個(gè)”。所以有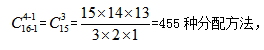
選擇A項(xiàng)。
小結(jié)2：隔板模型變形1：將n個(gè)相同的元素分給m個(gè)不同的對(duì)象，某些對(duì)象要求至少分k個(gè)元素（k≥2)，先給這些對(duì)象分k-1個(gè)元素，變型轉(zhuǎn)化為每個(gè)對(duì)象至少分1個(gè)，再進(jìn)行計(jì)算。
例3：將6本相同的作業(yè)本分給3名同學(xué)，每個(gè)同學(xué)都可以不分作業(yè)本，共有多少種分配方法？（ ）
A.28 B.36 C.40 D.48
【答案】A【解析】本題與例1相似，但也略有不同，區(qū)別在于同學(xué)可以不分作業(yè)本。因此可以先向每個(gè)同學(xué)借1本，共借到3本之后，本題就轉(zhuǎn)化成為“將9本相同的作業(yè)本分給3名同學(xué)，每人至少分1本”。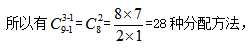
選擇A項(xiàng)。
小結(jié)3：隔板模型變形2：將n個(gè)相同的元素分給m個(gè)不同的對(duì)象，當(dāng)某些對(duì)象可以不分到元素時(shí)，先向這些對(duì)象分別各借1個(gè)，變形轉(zhuǎn)化為每個(gè)對(duì)象至少分1個(gè)，再進(jìn)行計(jì)算。
通過(guò)上述例題的介紹，相信同學(xué)們對(duì)于結(jié)合題目的不同變形要求，正確使用隔板模型有了一定的了解。舊書(shū)不厭百回讀，熟讀深思子自知。希望各位同學(xué)對(duì)于題目能反復(fù)練習(xí)和琢磨，做到舉一反三。
