行測數量關系：學會技巧，工程問題少煩惱
如何輕松解決工程問題
數量關系題目一直都是行測考試中的難點，并且也是大家學習上的痛點，而眾多題型中工程問題屬于難度較低的題型，因此大家可以先從工程問題入手。下面帶大家來學習工程問題的解決方法，以后在考試中輕松解決工程問題！
一、普通工程問題
解題策略：利用基本公式，工作總量=工作效率×工作時間，建立等量關系求解。
例1.某工程隊計劃在某一時間內修一條路。若每天修200米，則還剩下1000米；若每天修250米，則可多修200米。這條路總長是多少（ ）？
A.5800 B.6000 C.6200 D.6400
【答案】A【解析】題干描述了兩種不同方式完成同一個工程，故可以通過工作總量相等建立等量關系，由于時間未知，我們可以假設原計劃時間為t，第一種方式的工作總量表示為200t+1000，第二種方式為250t-200，200t+1000=250t-200，解得t=24天，代入第一種方式中總量200×24+1000=5800米。故本題選A。
二、多者合作問題
解題策略：梳理題干描述的不同合作方式，合理利用特值，再進行求解。
例2.一項工程，甲乙合作完成需要42天，乙丙合作完成需要30天，甲丙合作完成需要35天。現(xiàn)安排三人合作17天，然后由甲丙合作完成剩余工作，最后根據三人實際完成的工作量支付報酬。問丙獲得的報酬約為乙的多少倍（ ）？
A.1.7 B.1.9 C.2.1 D.2.3
【答案】C【解析】根據題意，設工作總量為42、30、35的最小公倍數210，則甲乙的工作效率之和為210÷42=5，乙丙的工作效率之和為210÷30=7，甲丙的工作效率之和為210÷35=6，則甲的效率為2，乙的效率為3，丙的效率為4。結合題目條件，三人合作17天，完成的工作量為（2+3+4）×17=153，剩余工作量為210-153=57，還需要57÷6=9.5天可以完成。乙實際完成的工作量為17×3=51，丙實際完成的工作量為（17+9.5）×4=106，則所求為106÷51≈2.1倍。故本題選C。
小妙招：題干給出多個主體的完工時間，將多個主體完工時間的最小公倍數設為工作總量，再進行求解。
例3.甲、乙兩人工作效率之比為3∶4。一項工作，甲單獨做需要120天剛好完成。現(xiàn)安排兩人合作，按照甲單獨工作2天、乙單獨工作2天、甲單獨工作1天、乙單獨工作1天……的順序交替工作，直至完成工作。問，乙一共工作了多少天（ ）？（不足一天按一天算）
A.50 B.51 C.52 D.53
【答案】B【解析】根據題意，設甲、乙兩人的工作效率分別為3和4，則工作總量為3×120=360。實際工作中，每2+2+1+1=6天一個周期，每個周期完成的工作量為3×2+4×2+3+4=21，360÷21=17……3，說明17個周期之后還剩下3的工作量，接下來輪到甲工作，剛好用1天完成剩余工作。則所求為17×（2+1）=51天。故本題選B。
小妙招：題干直接給出效率比，根據效率比設效率為未知數或特值，再進行求解。
相信通過上面題目，大家已經學會了工程問題的具體方法，希望大家勤加練習，在考試中輕松解決工程問題。
特值思想
行測考試中，很多人總覺得數量關系很難，但其實這部分中也有比較簡單的題目。今天就給大家介紹數量關系中的一個高頻，并且比較容易得分的知識點——工程問題。其解題方式多種多樣，特值思想就是其中的一種。只需理清楚題目本質，相信你也可以利用特值輕松解題。
一、基本公式
基本公式：工作總量（W）=工作效率（p）×工作時間（t）。
解題方法：特值法
二、例題展示
例1.一項工程，由甲、乙兩個隊合作10天可以完成，甲、丙兩隊合作15天可以完成，三隊合作8天可以完成。則乙和丙合作的效率是甲單獨做效率的多少倍（ ）？
A.2 B.1.5 C.1 D.3
【答案】A【解析】已知三種不同合作方式的完工時間，所以可將總量設為(10、15、8的最小公倍數)120，P甲+P乙=120÷10=12①，同理，P甲+P丙=8②，P甲+P乙+P丙=15③，聯(lián)立解得P甲=5，P乙=7，P丙=3，則(P乙+P丙)÷P甲=(7+3)÷5=2，選擇A項。
小結：當已知多個完工時間時，可將工作總量特值為完工時間的公倍數，進而將效率表示出來，再根據題意求解。
例2.某醫(yī)療器械公司為完成一批口罩訂單生產任務，先期投產了A和B兩條生產線，A和B的工作效率之比是2∶3，計劃8天可完成訂單生產任務。兩天后公司又投產了生產線C，A和C的工作效率之比為2∶1。問：該批口罩訂單任務將提前幾天完成（ ）？
A.1 B.2 C.3 D.4
【答案】A【解析】由題意可得，A、B、C的工作效率之比為2∶3∶1。則設A的工作效率為2，則B的工作效率為3，C的工作效率為1，生產任務總量為（2+3）×8=40。根據“兩天后公司又投產了生產線C”，可知A和B合作生產兩天，剩余任務量由A、B、C共同完成。設A、B、C的合作時間為t天，可得（2+3）×2+（2+3+1）×t=40，解得t=5，則完成全部任務共用2+5=7天，則該批口罩訂單任務將提前8-7=1天完成，選擇A項。
小結：在多者合作問題中，當題干中直接或者間接給出最簡效率比，則可以將工作效率特值為最簡比數值，再根據題意求解。
例3.某農場有36臺收割機，要收割完所有的麥子需要14天時間，現(xiàn)收割了7天后增加4臺收割機，并通過技術改造使每臺機器的效率提升5%。問收割完所有的麥子還需要幾天（ ）？
A.3 B.4 C.5 D.6
【答案】D【解析】已知多臺相率相同的機器合作完工，可設原來每臺收割機的效率是“1”，則改造后的效率為1.05。設還需t天完工，根據前后工作總量不變得36×14=36×7+（36+4）×1.05t，解得t=6，所以還需要6天，選擇D項。
小結：當題目中已知多個效率相同的元素（人/機器），可以將每個元素單位時間的工作量特值為“1”，進而求總量，再根據題意求其它。
以上便是工程問題中利用特值解題的常見形式，值得注意的是，在利用特值解題的同時，核心還是需要梳理出對應的合作完成方式，便可以快速求解。
比例法
工程問題是行測數量關系中較為常見的一種題型，通常我們會借助工作總量相等去構建等量關系進行求解，在做題的過程中我們也會通過賦值法求解，但是各位小伙伴有時也會發(fā)現(xiàn)單純地使用方程法和賦值法解題也較為復雜，今天就帶大家來學習一下比例法在工程問題中的應用。
首先，我們一起了解一下比例法在工程問題中的基本應用：
根據工程問題的基本公式W=P×T可知這三個量的比例關系：
1.當工作總量W一定時，工作效率P與工作時間T成反比；
2.當工作效率P一定時，工作總量W與工作時間T成正比；
3.當工作時間T一定時，工作總量W與工作效率P成正比。
其次，我們還需要明確比例法可使用的情況：
（1）存在不變量；
（2）題干中存在或可以得到比例關系；
兩個條件同時滿足的時候就可以使用比例法了。結合實際的應用，一般題干中涉及的工作總量不變，給出的工作效率的比例關系或者出現(xiàn)了工作效率的比例變化時，可根據效率和時間成反比得到時間的比例關系，然后進行求解（亦或者是得到時間比例關系，從而得到效率的比值）。
最后，進行一下實戰(zhàn)演練：
例1.為響應建設“綠色城市”的號召，某社區(qū)黨員義務植樹300棵，由于參加植樹的全體黨員植樹的積極性高漲，實際工作效率提高為原來的1.2倍，結果提前20分鐘完成任務，則原來每小時植樹多少棵（ ）？
A.120 B.150 C.135 D.125
【答案】B【解析】題目中總量保持不變且出現(xiàn)了工作效率的比值變化，則我們可以考慮用比例法求解。根據實際的工作效率為原來的1.2倍，可以得出——原來效率：實際效率=1：1.2=5：6；根據工作總量不變，效率和時間成反比可得——原來時間：實際時間=6：5，該比例代表著原來用6份時間，后來只需要用5份時間，少的1份時間既是對應題干中的“提前20分鐘”，即1份=20分鐘；則原來時間為：6份×20分鐘/份=120分鐘=2小時；由P=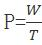
，可得原來的效率為300÷2=150。故本題選B。
例2.某印刷廠原計劃用全自動裝訂機花費4小時裝訂一批文件，但在還剩300份文件時裝訂機出現(xiàn)故障，無法裝訂。印刷廠立即安排了部分員工進行人工裝訂，由于人工裝訂的總效率僅為機器的20%，最終比原計劃推遲1小時完成裝訂，則這批文件共有（ ）份。
A.2400 B.3600 C.4800 D.6000
【答案】C【解析】對于剩余的300份文件，由于從機器裝訂變?yōu)槿斯ぱb訂，而導致了時間推遲——此過程中，總量不變，且存在工作效率的比例變化，故可以用比例法。對于最后的300份文件而言，根據條件“由于人工裝訂的總效率僅為機器的20%”可以得到——機器效率：人工效率=1∶0.2=5：1；則根據“完成相同工作量所需時間之比是效率的反比”可以得到——機器完成時間：人工完成時間=1：5，在該時間比例中，兩時間差4份，4份對應“推遲的1小時”，即4份=1小時，機器完成的時間需要1份時間，也就是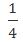
小時；也就是說機器完成300份文件需要
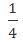小時，則機器效率為：300÷
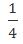=1200。再結合條件“機器全自動裝訂需要4小時完成”，可得這批文件共有1200×4=4800份。故本題選C。
通過以上兩題的演練可見，比例法解決工程問題還是比較快捷的，各位小伙伴可以多練習幾次，熟練掌握，這樣才能夠在較短的時間內拿到盡可能多的分數。
行測數量關系工程問題中的交替合作
在行測考試中，數量關系是讓眾多考生頭痛不已的內容，數量部分涉及內容廣泛，計算邏輯多變，是大家拉開分數差距的一部分內容。其實數量關系并不是所有的題目都晦澀難懂，能從中選出自己擅長的亦或是易于掌握的題型才是重中之重，像工程問題中的交替合作就是容易掌握的一類題型，接下來我們就一起來探索如何解決交替合作問題吧。
一、題型概述
交替合作即多個主體合作完成某項工程，合作過程中按一定規(guī)律進行輪流工作。
二、解題步驟
1.確定工作總量和各自的工作效率。若題目沒有直接給出工作總量，通常用特值法（將工作總量賦值為多個主體完工時間的公倍數）；
2.找到最小循環(huán)周期，并求出一個周期內的工作量之和；
3.求出周期數，并確定整周期之外剩余工作量所用時間；
4.根據實際問題求解。
例1.一條隧道，甲單獨挖要20天完成，乙單獨挖要10天完成。如果甲先挖1天，然后乙接替甲挖1天，再由甲接替乙挖1天……兩人如此交替工作。那么，挖完這條隧道共用多少天（ ）？
A.14 B.16 C.15 D.13
【答案】A【解析】設工作總量為甲、乙單獨完工時間20和10的最小公倍數20，則甲的效率為20÷20=1，乙的效率為20÷10=2。將2天視為一個周期，則每個周期的效率為1+2=3，20÷3=6……2，說明經過6個周期后，剩余工作量為2，接下來甲再工作1天，乙再工作半天即可完成全部剩余工作，總的工作時間為6×2+1+0.5=13.5天，結合選項來看，挖完這條隧道共用14天，故本題選擇A項。
例2.加工一批零件，甲單獨工作需要80小時，乙單獨工作需要120小時，甲乙丙三人合作需要50小時。每個人單獨工作時的效率要比與別人合作時高25%。現(xiàn)在按照第一天甲乙合作，第二天甲丙合作，第三天乙丙合作的順序輪班工作，每天工作8小時。當全部零件完成時，甲工作了多少小時（ ）？
A.50.4 B.48 C.26.4 D.24
【答案】A【解析】根據題意，設工作總量為80、120、50的最小公倍數1200，則甲單獨工作的效率為1200÷80=15，與別人合作時的工作效率為15÷（1+25%）=12；乙單獨工作的效率為1200÷120=10，與別人合作時的工作效率為10÷（1+25%）=8；三人合作時的工作效率之和為1200÷50=24，則丙與別人合作時的工作效率為24-12-8=4。甲乙合作的效率之和為12+8=20，甲丙合作的效率之和為12+4=16，乙丙合作的效率之和為8+4=12。按照題干要求，工作以3天為周期，前3天的工作總量為20×8+16×8+12×8=384，1200÷384=3……48，說明3個周期后，還剩下48的工作量，接下來輪到甲乙合作，還需要48÷20=2.4小時能夠完成。甲在每個周期內的工作時間為8+8=16小時，則所求為16×3+2.4=50.4小時，故本題選A。
經過以上題目的學習，大家會發(fā)現(xiàn)這類題型其實并不難，是有一定規(guī)律的，但需要大家多加練習，熟練掌握，才能更好地靈活應用。
