行測數(shù)量關(guān)系考點——抓住幾何問題的分數(shù)
幾何問題是行測數(shù)量關(guān)系中的高頻題型，如，正方形、長方形、圓形、三角形等平面圖形的周長和面積，以及正方體、長方體、球體、圓柱體等立體圖形的表面積和體積。還有一些是大家平時接觸比較少，容易忽視的圖形，如菱形、圓錐體。都是通過基本公式和性質(zhì)來解題。
常考題型
1.一般幾何問題（三角形、矩形、圓形、六邊形等）
2.幾何圖形最值問題（面積最大、怎樣走距離最短）
常考定理
1.兩個三角形高相等，面積之比等于其底邊長之比。
2.幾何等比放縮性質(zhì)：若邊長（或半徑）為n倍，則周長也為n倍，面積為n的2次方倍，體積為n的3次方倍。
3.周長一定，越接近圓，面積越大；反之，面積一定，越接近圓，周長越小；
4.表面積一定，越接近球，體積越大；反之，體積一定，越接近球，表面積越小。
5.兩點之間直線距離最短。
常用解題方法
畫圖，考慮特殊角度、圖形，做輔助線。
平面幾何
周長公式：
正方形：C=4a
長方形：C=2（a+b）
圓形：C=2πr
扇形：C=弧長+2r=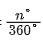
×2πr+2r
面積公式
正方形：S=a2
長方形：S=ab
圓形：S=πr2
扇形：S=πr2×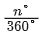
三角形：S=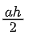
平行四邊形：S=ah
菱形：S=對角線乘積/2
梯形：S=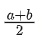
×h
立體幾何
表面積公式
正方體：S=6a2
長方體：S=2（ab+ac+bc）
球體：S=4πr2 =πD2
圓柱體：S=2πr2+2πrh
球：S=4πr2=πd2
體積公式
正方體：V=a3
長方體：V=abc
球體：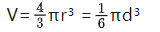
圓柱體：V=πr2h
圓錐：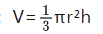
棱錐：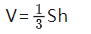
相似三角形理論
1.由圓周上某一點和圓的直徑所組成的三角形一定是直角三角形。
2.相似三角形：
①判定：兩個角相等，則兩個三角形相似；
②結(jié)論：對應(yīng)邊成比例；面積之比=邊長之比的平方。
3.勾股定理：a2+b2=c2
①常考勾股數(shù)：（3、4、5）、（6、8、10）、（5、12、13），當(dāng)直角三角形邊長為（6、8、10）、（5、12、13）時，其周長與面積相等；
②若直角三角形的三個角分別為30°、60°、90°時，則短直角邊是斜邊的一半；長直角邊是短直角邊的√3倍；
常用公式如下：
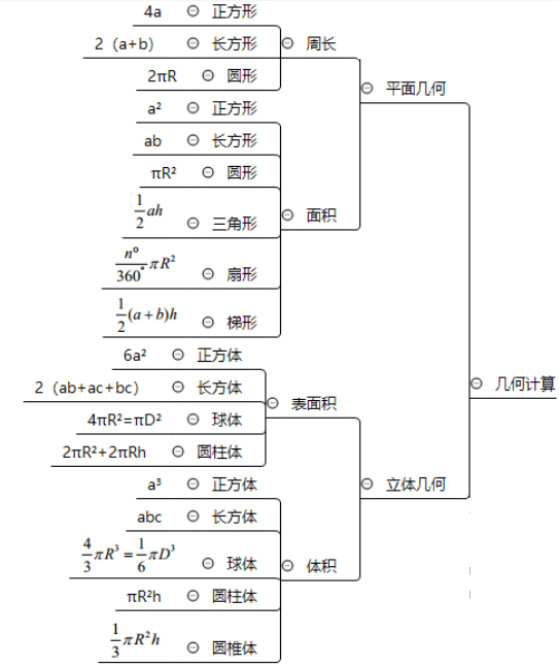
試題實例
1.一個長方形，若將短邊長度增加4厘米，長邊長度增加一倍，則面積是原來的3倍，若將長邊縮短8厘米，就成正方形，則原長方形面積是多少平方厘米（ ）？
A.180
B.128
C.84
D.48
【答案】B【解析】第一步，本題考查幾何問題，屬于平面幾何類。
第二步，設(shè)長方形的短邊為x厘米，由長邊縮短8厘米變成正方形可知，長為（x+8）厘米；根據(jù)面積是原來的3倍，可得2（x+8）×（x+4）=3（x+8）×x，解得x=8（厘米）。
第三步，故原長方形面積為（8+8）×8=128（平方厘米）。
因此，選擇B選項。
2.一個高為10厘米，底面半徑為5厘米的圓錐體塑料零件置于水中，底面朝上且水面平行，其浮出水面部分的高為2厘米。那么當(dāng)該零件底面朝下且與水面平行置于水中時，浮出水面部分的高在以下哪個范圍內(nèi)？（零件始終不接觸水底）（ ）
A．不到6厘米
B．6～7厘米之間
C．7～8厘米之間
D．超過8厘米
【答案】C【解析】第一步，本題考查幾何問題。第二步，露出水面的高度為2，說明水下高度為8，那么排水體積為圓錐體積的（8÷10）3=64/125，倒置后浮力相同，排水體積也為圓錐體積的64/125，那么水面上的體積為圓錐的61/125，高度為圓錐的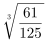
略小于0.8，故高度略低于8厘米。因此，選擇C選項。
3.下圖中，三個同心圓的半徑分別為1厘米、2厘米、3厘米，AB與CD垂直且過圓心O。那么圖中陰影部分面積與非陰影部分的面積之比是多少（ ）
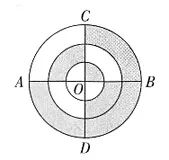
A.10:7
B.11:7
C.12:5
D.13:6
【答案】B【解析】將圖中非陰影部分進行移動拼合后發(fā)現(xiàn)，非陰影部分可以看作由四分之一個大圓、四分之一個中圓和四分之一個小圓構(gòu)成，面積為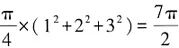
平方厘米，陰影和非陰影部分的總面積為32×π=9π平方厘米，則陰影部分面積為
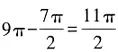，圖中陰影部分面積與非陰影部分的面積之比為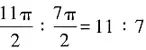
故本題選B。
