行測(cè)數(shù)量關(guān)系排列組合解題技巧
分類與分步
在各類公職考試的數(shù)量關(guān)系中，有一類比較特殊的問題——排列組合，之所以說特殊是因?yàn)樗R(shí)系統(tǒng)相對(duì)獨(dú)立，研究問題的方法與對(duì)象也有所不同。大家往往會(huì)覺得它很難，遇到就放棄，但排列組合是一類計(jì)數(shù)問題，簡(jiǎn)單來(lái)講就是統(tǒng)計(jì)方法數(shù)，還是有一些簡(jiǎn)單題的。那么，今天介紹的內(nèi)容——分類與分布，是排列組合問題中比較重要的一環(huán)，也是比較簡(jiǎn)單的一部分內(nèi)容。今天就和大家學(xué)習(xí)一下。
首先，我們要明確什么是分類與分步呢？他們是兩種不同的計(jì)數(shù)原理。
1.加法原理（分類計(jì)數(shù)）：做一件事情，完成它有N類方式，第一類方式有M1種方法，第二類方式有M2種方法，……，第N類方式有MN種方法，那么完成這件事情共有M1+M2+……+MN種方法。
2.乘法原理（分步計(jì)數(shù)）：做一件事，完成它需要分成n個(gè)步驟，做第一步有m1種不同的方法，做第二步有m2不同的方法，……，做第n步有mn不同的方法。那么完成這件事共有N=m1*m2*m3*…*mn種不同的方法
下面我們通過例題來(lái)學(xué)習(xí)如何通過常用方法求解排列組合問題。
例題1：若每天從甲地到乙地分別有4趟航班、6列火車、3班長(zhǎng)途汽車，則從甲地到乙地共有（ ）種不同的出行選擇。
A.13
B.22
C.27
D.72
【答案】A【解析】從甲地到乙地，任選一趟航班、一列火車或一班長(zhǎng)途汽車均能完成此事，是分類的過程。因此若想完成對(duì)“從甲地到乙地不同的出行選擇”的計(jì)數(shù)，可分類討論，結(jié)合題目描述，按不同出行方式分為三類：①坐飛機(jī)，有4種選擇；②坐火車，有6種選擇；③坐汽車，有3種選擇。分類相加，故共有4+6+3=13種不同的出行選擇，因此選擇A項(xiàng)。
例題2：將4個(gè)不同顏色的錦囊放入3個(gè)不同的錦盒里，如果允許錦盒是空的，則所有可能的放置方法有（ ）種。
A.7
B.12
C.81
D.64
【答案】C【解析】只放1個(gè)錦囊不能完成此事，放2個(gè)、3個(gè)也不能完成此事，必須4個(gè)錦囊都放入錦盒才能完成此事，是分步的過程。第一步，確定第1個(gè)錦囊的放法，放在任意一個(gè)盒子里都是可行的，所以有3種放法；第二步，確定第2個(gè)錦囊的放法，同樣放在任意一個(gè)盒子里都是可行的，所以也有3種放法；第三步，確定第3個(gè)錦囊的放法，同理有3種；第四步，確定第4個(gè)錦囊的放法，同理有3種。分步相乘，一共有3×3×3×3=81種不同的放法，選擇C項(xiàng)。
通過上邊兩道題，相信大家已經(jīng)能夠掌握分類與分步啦，接下來(lái)，讓我們來(lái)練習(xí)一下吧。
練習(xí)1：單位3個(gè)科室分別有7名、9名和6名職工。現(xiàn)抽調(diào)2名來(lái)自不同科室的職工參加調(diào)研活動(dòng)，則有（ ）種不同的挑選方式。
A.22
B.66
C.159
D.378
【答案】C【解析】從三個(gè)科室中選兩個(gè)科室共有三種分類方式：（7人，9人）、（7人，6人）、（6人，9人）。①選7人和9人的兩個(gè)科室，第一步，從7人的科室中選1人，有7種選擇，第二步，從9人的科室中選1人，有9種選擇，共有7×9=63種選擇。②選7人和6人的兩個(gè)科室，第一步，從7人的科室中選1人，有7種選擇，第二步，從6人的科室中選1人，有6種選擇，共有7×6=42種選擇。③選6人和9人的兩個(gè)科室，第一步，從6人的科室中選1人，有6種選擇，第二步，從9人的科室中選1人，有9種選擇，共有6×9=54種選擇。故共有63+42+54=159種挑選方式，因此選擇C項(xiàng)。
練習(xí)2：世界非物質(zhì)文化遺產(chǎn)高峰論壇召開記者會(huì)，共有10家國(guó)內(nèi)媒體和4家國(guó)外媒體參加。組委會(huì)從中選出3家媒體回答他們的問題，要求這3家媒體中既有國(guó)內(nèi)媒體又有國(guó)外媒體，且國(guó)內(nèi)外媒體交叉提問，則不同的提問方式有：（ ）
A.240種
B.360種
C.480種
D.1440種
【答案】C【解析】提問方式共有（國(guó)內(nèi)、國(guó)外、國(guó)內(nèi)）和（國(guó)外、國(guó)內(nèi)、國(guó)外）兩種順序。其中（國(guó)內(nèi)、國(guó)外、國(guó)內(nèi)）有10×4×9=360種；（國(guó)外、國(guó)內(nèi)、國(guó)外）有4×10×3=120種。共有360+120=480種，因此選擇C項(xiàng)。
相信通過今天的學(xué)習(xí)，大家已經(jīng)熟練掌握了分類與分步。希望大家在遇到排列組合問題后不再畏懼排列組合，把題干分析清楚，利用一些小技巧來(lái)解決排列組合問題。當(dāng)然大家還需要通過大量練習(xí)來(lái)真正熟練掌握這類方法，在解題過程中提升解題速度！
排列組合常用方法總結(jié)
優(yōu)限法
當(dāng)元素有絕對(duì)的位置要求時(shí)使用：第一步安排特殊元素，第二步解決其他元素。
例：一次會(huì)議某單位邀請(qǐng)了10名專家，該單位預(yù)定了10個(gè)房間，其中一層5間、二層5間。已知邀請(qǐng)專家中4人要求住二層、3人要求住一層、其余3人住任一層均可。那么要滿足他們的住房要求且每人1間，有多少種不同的安排方案（ ）？
A.75
B.450
C.7200
D.43200
【答案】D【解析】題干中4人要求住二層、3人要求住一層，優(yōu)先安排這7名專 家的房間，其余3人放在最后。4人要求住二層，其方法數(shù)為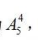
3人要求住一層，其方法數(shù)為
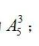其余3人安排住剩下的3個(gè)房間，其方法數(shù)為
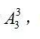故共有
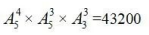種不同的安排方案。
捆綁法
當(dāng)元素必須相鄰時(shí)使用：第一步把相鄰元素看成一個(gè)整體（保證相鄰），并且和其他元素進(jìn)行排列，第二步確定整體內(nèi)元素的順序。
例：為加強(qiáng)機(jī)關(guān)文化建設(shè)，某市直機(jī)關(guān)在系統(tǒng)內(nèi)舉辦演講比賽，3個(gè)部門分別派出3、2、4名選手參加比賽，要求每個(gè)部門的參賽選手比賽順序必須相連，問不同參賽順序的種數(shù)在以下哪個(gè)范圍之內(nèi)（ ）？
A.小于1000
B.1000～5000
C.5001～20000
D.大于20000
【答案】B【解析】題干要求每個(gè)部門的參賽選手比賽順序必須相連，可以先把每 個(gè)部門的參賽選手分別捆綁起來(lái)看成3個(gè)整體進(jìn)行安排，再考慮部門內(nèi)部選手的順序。首先 考慮三個(gè)部門的出場(chǎng)順序，有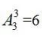
種；其次考慮每個(gè)部門選手的出場(chǎng)順序，分別有
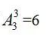種，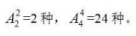
則不同參賽順序的種數(shù)為6×6×2×24=72×24，計(jì)算結(jié)果顯然大于1000，小于5000，故此題答案為B。
插空法
當(dāng)元素不能相鄰時(shí)使用：第一步安排不相鄰以外的元素（形成空隙），第二步將不能相鄰的元素插入空隙中（確保不相鄰）。
例：把12棵同樣的松樹和6棵同樣的柏樹種植在道路兩側(cè)，每側(cè)種植9棵，要求每側(cè)地柏樹數(shù)量相等且不相鄰，且道路起點(diǎn)和終點(diǎn)處兩側(cè)種植的都必須是松樹。問有多少種不同的種植方法（ ）？
A.36
B.50
C.100
D.400
【答案】C【解析】道路每側(cè)種植9棵樹，其中6棵松樹3棵柏樹，6棵松樹形成 5個(gè)空隙，選擇3個(gè)空隙并將3棵柏樹放入有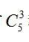
種方法，因?yàn)橛袃蓚?cè)，故共有
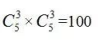種不同的種植方法。
間接法
當(dāng)正面解題情況復(fù)雜，而問題對(duì)立面情況比較容易計(jì)算時(shí)使用（題干出現(xiàn)“至少”“至多”等描述字眼）：第一步分別計(jì)算整體情況數(shù)和對(duì)立面的情況數(shù)，第二步將兩者做差。
例：某單位有甲和乙2個(gè)辦公室，分別有職工5人和4人。每周從這9名職工中隨機(jī)抽取1人下沉社區(qū)擔(dān)任志愿者（同一人有可能被連續(xù)、重復(fù)選中）。問7月前2周的志愿者至少有1人來(lái)自甲辦公室的安排有多少種（ ）？
A.65
B.81
C.16
D.32
【答案】A【解析】根據(jù)題意可知，7月前2周的志愿者總情況數(shù)為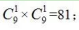
7 月前2周的志愿者均來(lái)自乙辦公室的情況數(shù)為
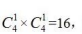因此所求81-16=65。
通過上面的方法介紹和對(duì)應(yīng)題目練習(xí)，相信大家對(duì)于排列組合的常用方法有了更深的理解，后續(xù)還是需要不斷鞏固練習(xí)，方能駕輕就熟，徹底地啃下這塊硬骨頭！
