行測備考-數(shù)量關(guān)系
生活中的統(tǒng)籌之排隊取水問題
統(tǒng)籌問題是用數(shù)學思維來研究人力、物力的運用和籌劃，以便發(fā)揮最大效率的一類問題。
統(tǒng)籌問題所包含的內(nèi)容非常繁雜，比如物資調(diào)運、工作分配、排隊等。這些都是我們在日常生活、工作中經(jīng)常碰到的問題，把它們安排得更快、更好、更合理，這就是統(tǒng)籌問題存在的最大意義。
要解決統(tǒng)籌問題，必須掌握統(tǒng)籌方法。所謂統(tǒng)籌方法，就是一種安排工作進程的數(shù)學方法，比如效率優(yōu)先原則就是其中一種。
而在統(tǒng)籌問題中有一類問題很有意思，就是排隊取水問題，我們通過幾道例題來看一下：
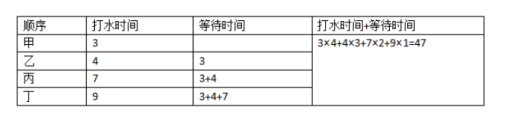
例1：甲、乙、丙、丁去排隊打水，4人打水所需的時間分別為3分鐘、4分鐘、7分鐘、9分鐘。如果只有一個水龍頭，要使甲、乙、丙、丁4人打水的時間與等待的時間之和最短，則這個最短時間是多少?
【解析】要使4人打水的時間與等待的時間和最短，讓等待時間最短即可，因為打水的時間是固定的，所以在只有一個水龍頭的情況下，肯定是打水時間最短的人先打，打水時間最長的后打，所以，4個人的打水順序是甲、乙、丙、丁。
變形：
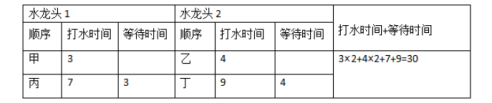
例2：在例1的基礎(chǔ)上，把“只有一個水龍頭”改為“可以同時使用2個水龍頭打水”。
【解析】要使4人打水的時間與等待的時間之和最短，只需讓等待時間最短即可，因為打水的時間是固定的，所以在有2個水龍頭的情況下，4個人的打水情況如下長:
例3：8個人去水房打水，8人打水所需的時間分別為2分鐘、3分鐘、5分鐘、7分鐘，11分鐘、13分鐘、17分鐘、19分鐘。如果水房只能同時打開3個水龍頭，要使8人打水的時間與等待的時間之和最短，則這個最短時間是多少?
【解析】按打水時間從小到大，把這8個人分別叫作:趙、錢、孫、李、周、吳、鄭和王。則這8個人的打水情況如下表:
大家發(fā)現(xiàn)解題規(guī)律了嗎?
①按照打水所需時間將時間按從大到小依次排開，
②照從1開始的自然數(shù)與排好的順序依次相乘，具體乘幾個數(shù)有幾個水龍頭決定。
同學們理清思路了嗎?
行測技巧之行程“不變”應“萬變”
行測考試行程題型一直作為考查重點，今天我們來看看考查了很多次的相遇問題，了解下二次相遇中追上也是相遇的奇妙過程，相信通過學習，這類題大家之后肯定能手到擒來!
一、什么是“追上即相遇”
甲、乙兩人分別從A、B兩地同時出發(fā)，相向而行，第一次相遇之后繼續(xù)前行，到達目的地后都立即返回。
問題1：若甲、乙的速度比為2:1，第二次相遇在哪?
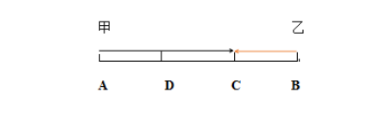
【解析】若甲、乙的速度比為2:1，時間一樣，路程比=速度比，則甲乙的路程比也為2:1(如下圖)，在C處相遇后繼續(xù)前行，保持路程比為2:1，則當甲到B地再返回時到達C點，乙應該到達D點;接著繼續(xù)前行，甲又走2份路程到達A點，此時乙走1份路程也到A點。
問題2：兩人速度比繼續(xù)擴大又會出現(xiàn)什么情況呢?
【解析】若甲、乙的速度比為3:1，時間一樣的前提下，路程比依然保持3:1(如下圖)：
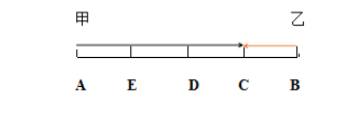
每當甲走3份路程，乙要走1份路程，則有，當甲返回途中到D時，乙也到D，此時兩人方向相同，甲從背后追上了乙，在還沒來得及發(fā)生第二次迎面相遇時就已經(jīng)追上了。
問題3：哪些題的二次相遇屬于這種情況呢?
【解析】回顧上邊兩個例子，發(fā)現(xiàn)結(jié)論：速度比一旦超過2:1，則存在第二次追上即相遇。
二、初識“追上即相遇”
上午9點整，甲從A地出發(fā)，騎自行車去B地，乙從B地出發(fā)，開車去A地。兩人第一次相遇時為9點半，甲、乙到達目的地后都立即返回。若甲、乙的速度比為1∶3，則他們第二次相遇時為：
A.9:40 B.9:50 C.10:00 D.10:10
E.10:20 F.10:30 G.10:40 H.10:50
【解析】已知甲乙速度比1:3，則存在第二次追上即相遇，根據(jù)題目描述作行程圖如下：
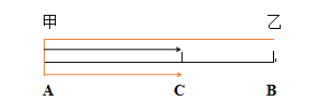
從出發(fā)直接到第二次追上(在C處)，由行程圖知甲乙的路程差固定為全程AB距離，由追及基本公式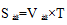
知，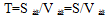
,而全程S是第一次相遇甲乙兩人的路程和，從九點出發(fā)到九點半第一次相遇，時間是30分鐘，所以
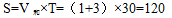。則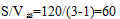
,九點出發(fā)，60分鐘后第二次追上，故第二次相遇時為10:00。本題選C。
在第二次追上即相遇的題目中，從出發(fā)到第二次追上，路程差恒定不變，固定是一個全程，找到這一不變，一切難點迎刃而解!
三、鞏固訓練
甲、乙二人分別從A、B兩地同時出發(fā)，相向而行，甲的速度是乙的4倍，甲用時15分鐘到達B地后立即返回，甲乙第二次相遇后，乙再走( )分鐘才能到達A地。
A.40 B.30 C.45 D.33.3
【解析】速度比4:1，則第二次存在追上即相遇，從出發(fā)到第二次追上作行程圖如下：
路程差固定為一個全程S，用時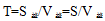
，由于題目已知甲走全程用時15分鐘，所以
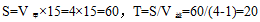,所求時間為乙走全程時間減去20分鐘，全程一定，甲乙速度是4:1，時間呈反比，則甲乙時間之比為1:4,1份對應甲走全程的15分鐘，故4份對應60分鐘，即乙走全程用時60分鐘，所求即為60-20=40，本題選A。
以上就是關(guān)于相遇問題的解決技巧，相信你已經(jīng)找到這類題的法寶了，動動手指，勤做練習吧!
均值不等式在極限思維中的運用
同學們對于極限思維這個概念都不陌生，極限思維其實在指用極限狀態(tài)分析問題和解決問題的一種數(shù)學思維，簡單來說就是求最大值或者最小值問題。那均值不等式在極限思維中如何體現(xiàn)的呢，這一類型的題型特征是什么呢以及如何掌握它的解題思路，是同學們相對比較關(guān)心的內(nèi)容，讓我們一起來學習一下吧。
一、均值不等式的題型特征
均值不等式是屬于極值問題中的一個運用，也是可以用極限思維來解題的，一般在題干或者問法中出現(xiàn)最大或最小，最多或最少、至多或至少。
二、均值不等式的定理
均值不等式的定理，若a、b是實數(shù)，則a2+b2≧2ab，符號當且僅當a=b的時候取得。一般適用于兩種題型，(1)當和一定時，求積的最大值，也就是若a、b均是正實數(shù)，則
，符號當且僅當a=b的時候取得。但如果兩個數(shù)a、b取不到相等的時候，和一定的兩個數(shù)，差越小，積越大。(2)當積一定，求和的最小值，同理，如果兩個數(shù)a、b取不到相等的時候，積一定的兩個數(shù)，差越小，和越小。
三、例題展示
例1、若兩個自然數(shù)的和為20，求這兩個自然數(shù)積的最大值。
答案為100。解析：根據(jù)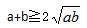
，等號當且僅當a=b的時候取得。可得
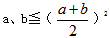，ab要取得最大值僅當a=b的時候取得，所以這兩個數(shù)分別都是10，他們的積取到最大，且最大值為100。
例2、用60米長的鐵板圍成一個長方形雞窩，問這個雞窩的面積最大是多少?
A、200 B、225 C.300 D、600
答案B。解析：由長方形的周長為60，可知長方形的長加寬的和為60÷2=30，兩個數(shù)的和一定時，當且僅當這兩個數(shù)相等時，這兩個數(shù)的積可取得最大值，也就是長等于寬等于30÷2=15，所以雞窩的面積最大為長乘以寬等于15×15=225。
