提升行測(cè)數(shù)量關(guān)系方法學(xué)習(xí)
行測(cè)數(shù)量關(guān)系：方程之其“舉足輕重”
數(shù)學(xué)運(yùn)算是公職考試中不可或缺的一部分，同時(shí)數(shù)學(xué)運(yùn)算也成了大多數(shù)考生備考過(guò)程中的一塊硬石頭。本文帶各位考生一起碰碰這個(gè)硬石頭，如此硬石頭用軟拳頭“方程”解決最為妙不可言，所以方程法在數(shù)量關(guān)系的題目解決過(guò)程中是有著“舉足輕重”的地位的。
例題：六一兒童節(jié)期間，100名幼兒園學(xué)生參加5項(xiàng)活動(dòng)，參加人數(shù)最多的活動(dòng)人數(shù)不超過(guò)參加人數(shù)最少的活動(dòng)人數(shù)的二倍，則參加人數(shù)最少的活動(dòng)最少有多少人參加？
【解析】在這道題目中我們已知參加5項(xiàng)活動(dòng)的總?cè)藬?shù)100，同時(shí)，題目問(wèn)的是參加人數(shù)最少的活動(dòng)最少有多少人參加。屬于和一定求某個(gè)數(shù)的最小值。那要保證某項(xiàng)活動(dòng)參加人數(shù)最少，其他活動(dòng)的參加人數(shù)要盡可能多。然而在這道題目中并沒(méi)有規(guī)定每項(xiàng)活動(dòng)的參加人數(shù)要互不相等，所以要讓參加活動(dòng)人數(shù)最少的項(xiàng)目參加人數(shù)最少我們可已讓其他項(xiàng)目的參加人數(shù)相等且都等于最多的那一項(xiàng)的人數(shù)，因?yàn)閰⒓尤藬?shù)最多的活動(dòng)人數(shù)不超過(guò)參加人數(shù)最少的活動(dòng)人數(shù)的二倍，所以最多的項(xiàng)目參加人數(shù)最多應(yīng)該等于參加人數(shù)最少的活動(dòng)人數(shù)的二倍。假設(shè)參加人數(shù)最少的活動(dòng)人數(shù)為X，那其他項(xiàng)目的參加人數(shù)均為2X，則有X+2X+2X+2X+2X=100，9X=100，X≈11.1。有因?yàn)閄代表的是參加人數(shù)最少的活動(dòng)的參加人數(shù)，所以應(yīng)該為整數(shù)，那么X應(yīng)該為不小于11.1的整數(shù)，那X最小應(yīng)該取到12。
例題：某玩具廠車間生產(chǎn)一批玩具，原計(jì)劃每天生產(chǎn)100個(gè)，但實(shí)際生產(chǎn)過(guò)程中每天的生產(chǎn)量為120個(gè)。結(jié)果提前4天完工，還多生產(chǎn)了80個(gè)，則該玩具廠原計(jì)劃生產(chǎn)玩具( )個(gè)？
【解析】在這道題目中，可根據(jù)原計(jì)劃工作量和實(shí)際完成工作量之間的關(guān)系，建立等量關(guān)系，設(shè)原計(jì)劃生產(chǎn)t天，則原計(jì)劃生產(chǎn)100t個(gè)零件，根據(jù)“實(shí)際多生產(chǎn)了80個(gè)”，可得100t+80=120(t-4)，解得t=28，即原計(jì)劃生產(chǎn)28天，故原計(jì)劃生產(chǎn)零件100t=100×28=2800個(gè)。
例題：軟件園投入一筆資金用于獎(jiǎng)勵(lì)院內(nèi)優(yōu)秀企業(yè)。如果評(píng)出的優(yōu)秀企業(yè)占總企業(yè)數(shù)的10%，每家獎(jiǎng)勵(lì)100萬(wàn)元，資金將結(jié)余150萬(wàn)元；如果評(píng)出的優(yōu)秀企業(yè)占25%，每家獎(jiǎng)勵(lì)50萬(wàn)元，則還需要額外投入200萬(wàn)元。問(wèn)軟件園共有多少家企業(yè)？（ ）
【解析】在這道題目中，可根據(jù)計(jì)劃投入的獎(jiǎng)金預(yù)算一定，建立等量關(guān)系，假設(shè)軟件園共有X家企業(yè)，軟件園投入資金前后保持不變，根據(jù)題意有10%X×100+150=25%X×50-200，解得X=140。
通過(guò)以上三個(gè)題目可以看出，在數(shù)量關(guān)系中多種題型均可借助基本方程來(lái)解決。
行測(cè)數(shù)量關(guān)系之牛吃草問(wèn)題
在行測(cè)數(shù)量關(guān)系的備考中，部分考生碰到小題型時(shí)總是手足無(wú)措，在解決了一個(gè)題目之后卻不能舉一反三，達(dá)不到復(fù)習(xí)的效果。本文將向各位考生介紹小題型之一：牛吃草問(wèn)題，牛吃草問(wèn)題這種題型的特點(diǎn)是非常明顯的，真正弄懂了以后，這些看起來(lái)有難度的題都會(huì)迎刃而解了！
先來(lái)看一道牛吃草問(wèn)題的典型例題：
例題：牧場(chǎng)上有一片青草，每天都生長(zhǎng)得一樣快。這片青草供給10頭牛吃，可以吃22天，或者供給16頭牛吃，可以吃10天，期間一直有草生長(zhǎng)。如果供給25頭牛吃，可以吃多少天？（ ）
A.5 B.5.5 C.6 D.6.5
【答案】B。【解析】假設(shè)草繼續(xù)生長(zhǎng)，牛在吃，相當(dāng)于是在牛在追草，屬于追及問(wèn)題，結(jié)合追及問(wèn)題基本計(jì)量關(guān)系，那么追及距離即原有草量=牛吃的草量-草新生長(zhǎng)的量，則原有草量=(牛每天吃掉的草量-每天生長(zhǎng)的草量)×天數(shù)；設(shè)每頭牛每天吃一份草，草每天長(zhǎng)x份，可以供25頭牛吃t天，則有(10-x)×22=(16-x)×10=(25-x)t，解此方程即得x=5，t=5.5。
根據(jù)例題發(fā)現(xiàn)，此類問(wèn)題均屬追及問(wèn)題，結(jié)合原有草量=(牛每天吃掉的草量-每天生長(zhǎng)的草量)×天數(shù)，所以可以總結(jié)出牛吃草問(wèn)題的解題公式：(N1-x)×T1=(N2-x)×T2=(N3-x)×T3；那么如何識(shí)別是不是牛吃草問(wèn)題呢，其實(shí)不見(jiàn)得必須有牛有草，只要符合以下三個(gè)特征即可：
(1)存在類排比句；
(2)原有量為定值；
(3)有兩個(gè)因素的制約。
我們?cè)倏磧傻谰毩?xí)題檢驗(yàn)一下學(xué)習(xí)效果。
例1：某水庫(kù)共有10個(gè)泄洪閘，當(dāng)10個(gè)泄洪閘全部打開(kāi)時(shí)，8小時(shí)可將水位由警戒水位降至安全水位；只打開(kāi)6個(gè)泄洪閘時(shí)，這個(gè)過(guò)程為24個(gè)小時(shí)，如水庫(kù)每小時(shí)的入庫(kù)量穩(wěn)定，問(wèn)如果打開(kāi)8個(gè)泄洪閘時(shí)，需要多少小時(shí)可將水位降至安全水位？（ ）
A.10 B.12 C.14 D.16
【答案】B。【解析】設(shè)泄洪閘每小時(shí)泄洪量為1，水庫(kù)每小時(shí)的入庫(kù)量為x，所求為t小時(shí)。根據(jù)牛吃草問(wèn)題的公式有：(10-x)×8=(6-x)×24=(8-x)×t，解得x=4，t=12。
例2：某河道由于淤泥堆積影響到船只航行安全，現(xiàn)由工程隊(duì)使用挖沙機(jī)進(jìn)行清淤工作，清淤時(shí)上游河水又會(huì)帶來(lái)新的泥沙(假定每天的泥沙量恒定)。若使用1臺(tái)挖沙機(jī)300天可完成清淤工作，使用2臺(tái)挖沙機(jī)100天可完成清淤工作。為了盡快讓河道恢復(fù)使用，上級(jí)部門要求工程隊(duì)25天內(nèi)完成河道的全部清淤工作，那么工程隊(duì)至少要有多少臺(tái)挖沙機(jī)同時(shí)作？（ ）
A.4 B.5 C.6 D.7
【答案】D。【解析】設(shè)每臺(tái)挖沙機(jī)每天挖泥量為1，每天新增泥沙量為x，如果25天完成任務(wù)需要n臺(tái)挖沙機(jī)，則根據(jù)“清淤工作開(kāi)始時(shí)堆積的泥沙量相等”可列方程(1-x)×300=(2-x)×100=(n-x)×25，解得x=0.5，n=6.5，因此至少需要7臺(tái)。故本題選D。
通過(guò)以上的學(xué)習(xí)，相信大家對(duì)牛吃草問(wèn)題已經(jīng)有所了解，以后遇到符合題型特征的題目，直接代入公式進(jìn)行求解即可。
突破行測(cè)瓶頸 拿下數(shù)量關(guān)系
很多考生在行測(cè)備考過(guò)程中對(duì)于數(shù)量關(guān)系無(wú)從下手，也往往是因?yàn)閿?shù)量關(guān)系的影響，遲遲無(wú)法突破瓶頸。那么究竟能否通過(guò)科學(xué)高效的備考，決勝數(shù)量關(guān)系，實(shí)現(xiàn)行測(cè)成績(jī)的彎道超車呢？今天就給大家介紹下數(shù)量關(guān)系科學(xué)高效備考的四大步驟。
一、夯實(shí)基礎(chǔ)：解題方法學(xué)習(xí)
工欲善其事必先利其器。行測(cè)考試時(shí)間緊，題量大，數(shù)量關(guān)系題目技巧性強(qiáng)，所以高效備考的第一步就是學(xué)習(xí)常用的解題方法，尤其是具有普適性、能夠解決多種題型的方法。
二、重點(diǎn)突破：常考題型學(xué)習(xí)
知己知彼方能百戰(zhàn)不殆。備考的第二步就是逐個(gè)突破常考題型，緊緊抓住“考什么，學(xué)什么”的基本原則。
數(shù)量關(guān)系重點(diǎn)考察的題型主要有計(jì)算問(wèn)題(整除、和差倍比、等差數(shù)列、周期循環(huán)、簡(jiǎn)單計(jì)算等)、行程問(wèn)題(環(huán)形相遇、牛吃草、普通行程、流水行船)、工程問(wèn)題(多者合作)、幾何問(wèn)題(基本公式、解直角三角形、圖形相似)、排列組合(常用方法和隔板模型)、概率問(wèn)題(古典概率、幾何概率、多次獨(dú)立重復(fù)試驗(yàn))、利潤(rùn)問(wèn)題、容斥問(wèn)題、極值問(wèn)題。其中計(jì)算問(wèn)題、排列組合、概率問(wèn)題、幾何問(wèn)題更是重中之重。
在行測(cè)數(shù)量關(guān)系備考過(guò)程中，既要了解各種常考題型涉及的知識(shí)點(diǎn)，又要熟知常用的解題方法。
三、提升速度：題海強(qiáng)化訓(xùn)練
數(shù)量關(guān)系做題效率尤為重要，第三步就是通過(guò)刷題，提升大家的題感和知識(shí)掌握的熟練程度，基本在1-2分鐘左右完成一道題目。
具體操作是分成兩個(gè)階段，第一階段分題型進(jìn)行訓(xùn)練，目的是進(jìn)一步鞏固各種題型的知識(shí)點(diǎn)，真正吃透，熟能生巧；第二階段和省考題量一致設(shè)置套題，限定時(shí)間，培養(yǎng)題感，提升做題效率。
每次的訓(xùn)練完成之后，做好易錯(cuò)點(diǎn)的整理，形成錯(cuò)題筆記，發(fā)現(xiàn)自身弱項(xiàng)，中間穿插理論回顧，重點(diǎn)強(qiáng)化學(xué)習(xí)，難點(diǎn)逐個(gè)突破。
四、判斷取舍：如何選擇題目
備考第四步是提高對(duì)題目類型和難度的判斷能力，同時(shí)掌握選題技巧，在做題過(guò)程中由易到難，避免“死磕”難題，得不償失，在有限的時(shí)間內(nèi)最大限度的得到數(shù)量關(guān)系的分?jǐn)?shù)。
選題建議如下：選擇前2-3題，一般中等難度偏下；選擇題干短、數(shù)據(jù)少的題目；選擇熟悉且普遍難度不大的題型，如計(jì)算、利潤(rùn)、行程、工程等。最后，再做其他信息量多、難度較大的題目。
大家需要在平時(shí)的訓(xùn)練中，培養(yǎng)對(duì)題目的敏感性并強(qiáng)化選題技巧，真正的從戰(zhàn)術(shù)上多得到分?jǐn)?shù)。
相信通過(guò)以上四步，各位考生能夠提高數(shù)量關(guān)系備考效率，打破桎梏，突破瓶頸，真正的在數(shù)量關(guān)系上實(shí)現(xiàn)成績(jī)的彎道超車。
行測(cè)排列組合不求人，隔板模型直接套
在行測(cè)考試中，數(shù)量關(guān)系雖然題量不多，但分值卻不少。考試時(shí)間緊，很多同學(xué)又主觀認(rèn)為數(shù)量關(guān)系偏難，往往不給數(shù)量機(jī)會(huì)，尤其在面對(duì)數(shù)量關(guān)系中的常考題型排列組合時(shí)，在備考時(shí)都會(huì)選擇性的避開(kāi)，但其實(shí)排列組合中有一種比較典型的隔板模型，相對(duì)于其他的排列組合的題目來(lái)說(shuō)，難度不大，只要掌握他的本質(zhì)，就能融會(huì)貫通啦。接下來(lái)就帶大家一起來(lái)學(xué)習(xí)一下隔板模型的相關(guān)知識(shí)吧！
一、什么是隔板模型
隔板模型本質(zhì)上是同素分堆的問(wèn)題，即將n個(gè)相同的元素分給m個(gè)不同的對(duì)象，每個(gè)對(duì)象至少分到一個(gè)元素，且要分完，問(wèn)有多少種不同分法的問(wèn)題。
二、隔板模型的條件
1.所分的元素必須完全相同
2.所要分的元素必須分完
3.每個(gè)對(duì)象至少分到1個(gè)
三、隔板模型的相關(guān)應(yīng)用
例1：將9個(gè)完全相同的小球分給3個(gè)小朋友，要求每個(gè)小朋友必須分到至少一個(gè)球，球要分完，總共有多少種分法？（ ）
A.19 B.24 C.28 D.30
【解析】這個(gè)題滿足隔板模型的所有條件，那要怎么樣去思考呢？我們可以考慮先將小球一字排開(kāi)，如圖所示
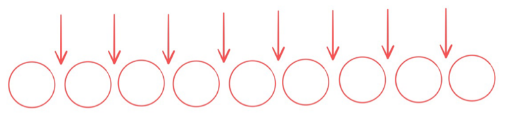
此時(shí)我們觀察到9個(gè)小球除了端頭兩個(gè)位置以外，會(huì)形成8個(gè)空位，也就是箭頭所標(biāo)注的位置，如果我們?nèi)蓧K板插入這8個(gè)空中的其中任意兩個(gè)空位，都可以將這9個(gè)小球分成三份，并且滿足每一份至少有一個(gè)小球，再把這三份分給三個(gè)小朋友，就可以滿足每人至少一個(gè)球且球分完，所以8個(gè)空插兩塊板就共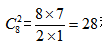
種情況。選擇C選項(xiàng)。
由上題總結(jié)可得，若將n個(gè)相同元素分成m份，每份至少一個(gè)元素，共有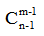
種情況。
例2：小明要將30個(gè)一模一樣的玩具球放入3個(gè)不同顏色的桶里面，每個(gè)桶至少放9個(gè)玩具球，問(wèn)一共有多少種不同的放法？（ ）
A.12 B.11 C.10 D.9
【解析】此題直觀的來(lái)看不滿足隔板模型當(dāng)中每個(gè)對(duì)象至少分一個(gè)的條件，但是可以通過(guò)轉(zhuǎn)換使之滿足，即給每個(gè)桶先放8個(gè)玩具球，剩下30-3×8=6個(gè)小球，再放到3個(gè)桶里，就可以將此題轉(zhuǎn)化為“將6個(gè)玩具球放到三個(gè)桶里，每個(gè)桶至少放一個(gè)球”，所以利用公式共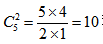
種分法，選C。
以上就是排列組合問(wèn)題當(dāng)中的隔板模型的解法及相關(guān)變形應(yīng)用的巧解方式，所以了解隔板模型的本質(zhì)后，這一類題型并不難，通過(guò)本文的講解，你能識(shí)別出隔板模型的考察了么？希望各位考生在備考時(shí)打好堅(jiān)實(shí)的基礎(chǔ)，靈活使用各種方法解決這一類題目。
