
行測數(shù)量關(guān)系之利潤問題、貨物集中問題、工程問題解題技巧
利潤問題:“小”表格,“大”作用
行測數(shù)量關(guān)系由于考點繁多,且部分考點的題目難度相對較大,于是諸多考生望而卻步。但是行測想要拿高分,數(shù)量關(guān)系部分就顯得尤為重要,本次給各位考生分享一個相對容易且測查頻率較高的題型——利潤問題。
一、什么是利潤問題?
利潤問題是一類主要研究在交易過程中有關(guān)成本、售價、利潤、利潤率等概念之間計算關(guān)系的問題。
二、怎么解利潤問題?
利潤問題考試過程中主要使用基本公式、方程法以及表格法進行解決,常考基本公式有:
利潤=售價-成本
利潤率=利潤/成本×100%=(售價-成本)/成本×100%=售價/成本-1
售價=成本×(1+利潤率)
成本=售價÷(1+利潤率)
然而很多利潤問題的題干描述較長,對于考生來說比較棘手的問題就是讀題分析題干,今天我們重點通過幾道題目向大家展示如何借助表格法快速清晰的額梳理題干,解決問題。
例1
某集團旗下有量販?zhǔn)匠泻捅忝裥〕袃煞N門店,集團統(tǒng)一采購的A商品在量販?zhǔn)匠泻捅忝裥〕械膯蝺r售價分別為12元和13.5元。4月A商品在兩種門店分別售出了600件和400件,共獲利5000元,問:該商品進價為多少元?( )
A.7.2 B.7.6 C.8.0 D.8.4
【答案】B【解析】通過題目描述可知題目中出現(xiàn)兩種銷售方式:“量販?zhǔn)匠小薄氨忝裥〕小保环猎诒砀裰袑⑦@兩種方式表示出來,進而表示出兩種方式的售價分別是12元和13.5元以及各自的銷量600件和400件,并且給出總利潤為5000元,需注意:總利潤=總售價-總成本,但是題中沒有給出成本,所以,不妨設(shè)單件成本為x;則有:

12×600+13.5×400-(600+400)×x=5000,解得x=7.6。
故答案選擇B項。
例2
服裝店買進一批童裝,按每套獲利50%定價賣出這批童裝的80%后,按定價的八折將剩下的童裝全部賣出,總利潤比預(yù)期減少了390元。問服裝店買進這批童裝花了多少元?( )
A.5500 B.6000 C.6500 D.7000
【答案】C【解析】通過題目可知這批童裝在銷售時分為打折前和打折后兩個階段,所以不妨在表格中將這兩個階段表示出來,接著題目說“按每套獲利50%定價賣出這批童裝的80%”,此時給出打折前的利潤率為50%,需注意:利潤率=售價/成本-1;此時如果設(shè)成本為y,則剛開始的定價應(yīng)為1.5x;同時已知打折前賣出80%,其實也就是總銷量的80%,但總銷量未知,所以如果設(shè)總銷量為x,則打折前售出0.8y,之后“定價的八折將剩下的童裝全部賣出”,即打折后的售價應(yīng)為:1.5x×0.8=1.2x,同時打折后的銷量為1-0.8y=0.2y,最后題目給出等量關(guān)系“總利潤比預(yù)期減少了390元”,其實就是:按原定價銷售完的總利潤-(打折前的總利潤+打折后的利潤)=390元。之前已表示出兩個階段的成本、售價、銷量;所以兩個階段分別的總利潤=單套利潤×銷量;而單套利潤=售價-成本,把出現(xiàn)的基本概念全部表示在表格中,再根據(jù)等量關(guān)系就有:
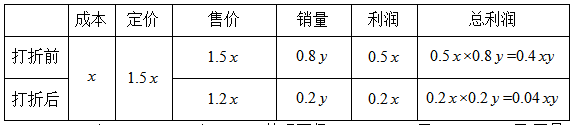
0.5xy-(0.4xy+0.04xy)=390,整理可得0.06xy=390元,xy=6500元,而最終題目求:“服裝店買進這批童裝花了多少元?”即求這批服裝的總成本,總成本=單件成本×總銷量=xy=6500元,故答案選擇C項。
通過以上兩道題可以看出來,不管題干中的銷售方式有多復(fù)雜,只要在讀題的過程中能夠結(jié)合表格法把其中的成本、定價、售價、銷量、利潤等梳理清楚,問題就可以迎刃而解。表格一出,問題解決,各位考生,動起來吧!
數(shù)量關(guān)系之貨物集中“取點看”
在行測考試當(dāng)中,數(shù)量關(guān)系往往是比較難的一部分內(nèi)容,尤其是統(tǒng)籌問題,它需要我們利用數(shù)學(xué)來研究人力、物力的運用和籌劃,使它們能發(fā)揮最大效率。此類問題對思維的要求比較高,往往研究的內(nèi)容看似復(fù)雜但是技巧性很強。今天帶大家來學(xué)習(xí)統(tǒng)籌問題常考的一種類型——貨物集中。
貨物集中問題:是一類集中統(tǒng)籌問題,是指將貨物集中的同時,求解如何集中能夠使得運費最少。
解題原則:確定一點,判斷該點兩端貨物的重量,把輕的一端向重的一端集中。在操作過程中我們無需考慮各位置之間的距離,只需考慮貨物的重量即可。接下來,我們通過一道例題來詳細(xì)說明此類題目如何快速求解。
例題
一條直線上依次有甲乙丙丁四個煤場,相鄰兩個煤場之間的距離都是3千米,目前甲有煤100噸,乙有煤90噸,丙有煤12噸,丁沒有煤。現(xiàn)在要將四個煤場的煤集中到一個煤場,已知1噸運輸1千米的花費是10元,那么為使得運費最少,則應(yīng)該把煤集中到哪個煤場?( )
A.甲 B.乙 C.丙 D.丁
【答案】B【解析】運輸單價不變,相鄰兩個煤場之間的距離固定,將輕的一端向重的一端更劃算,無需考慮距離。在甲和乙之間確定一點,則左邊貨物共100噸,右邊的貨物共102噸,因此往右邊集中即乙、丙或丁,排除A選項。再從乙丙之間確定一點,左邊總重190,右邊總重12,根據(jù)解題原則應(yīng)向左集中,故乙為最合適的集中位置,故選B。
掌握了貨物集中問題的解題原則,我們來通過兩道練習(xí)題練習(xí)鞏固一下。
練習(xí)1
在一條公路上每隔10里有1個集散地,共有5個集散地。其中1號集散地有旅客10人,3號集散地有旅客25人,5號集散地有45人,其余兩個集散地沒有人。如果要把所有人集中到一個集散地,那么所有旅客所走的總里數(shù)最少是多少?( )
A.1100 B.900 C.800 D.700
【答案】B【解析】讀完題后我們發(fā)現(xiàn)這道題的本質(zhì)也是貨物集中問題,因此先根據(jù)貨物集中的解題原則先去確定最優(yōu)的集散地然后再去計算。首先把點取在1號和2號之間,左邊有10人,右邊有70人,往多的一端即右邊集中,而2號沒有人,所以將點設(shè)在2號、3號之間與1號、2號之間相同。再把點取在3號和4號之間,左邊有35人,右邊有45人,往多的一端即右邊集中。而4號集散地沒有人,同理將點繼續(xù)往右邊集中,移動到了5號集散地。故該地為最優(yōu)集散地。計算總里數(shù)為:10×40+25×20=900。
故答案選B。
練習(xí)2
某個公司在甲、乙、丙三個地方各有一個倉庫,三個地方在一條直線上,之間距離分別相距6km,10km,甲倉庫有5噸貨,乙倉庫有8噸貨,丙倉庫有12噸貨,如果把所有的貨物集中到一個倉庫,每噸貨物每千米運費是100元,請問把貨物放在哪個倉庫最省錢?運費最少為多少?( )
A.甲、12000 B.乙、13000 C.丙、14000 D.乙、15000
【答案】D【解析】在甲乙之間確定一點,左邊總重5噸,右邊總重20噸,最省錢地應(yīng)為乙或丙,排除A。接著在乙丙之間取一點,左邊總重13噸,右邊總重為12噸,根據(jù)解題原則,應(yīng)該向左移動,所以確定將位置定在乙倉庫最省錢。其運費為5×100×6+12×100×10=15000。故本題選D。
通過以上例題的精講和展示,會發(fā)現(xiàn)只要掌握好了貨物集中的問題的解題思路,這樣大家會發(fā)現(xiàn)不僅可以很大程度地縮減我們每個距離、價格的計算的過程,也能提高正確率和準(zhǔn)確率,那么希望以后考生們多多地加強這類型題目的方法的思維,做到舉一反三,則以后遇到這類問題就可以迎刃而解。
三種特值告訴你工程問題可以很簡單
工程問題在行測數(shù)量關(guān)系的題目中經(jīng)常出現(xiàn),并且相對來說是比較簡單的,只要我們掌握了一定方法會發(fā)現(xiàn)這一類題目其實還是值得一做的。因此通過幾個例題來告訴大家,工程問題到底怎么來解決。
例1
一項工程,甲單獨做要10天,乙單獨做要15天。若甲、乙兩人合作,需要多少天?( )
A.5 B.6 C.7 D.8
【答案】B【解析】這道題中,我們會發(fā)現(xiàn)題目中出現(xiàn)了甲完成此項工程的時間,也出現(xiàn)的乙完成此項工程的時間,那我們想要求出合作的時間就需要知道此項工程的工作量和甲、乙的工作效率,所以這里不妨我們設(shè)總工作量為“1”。則甲的工作效率為1/10,乙的效率為1/15,因此合作效率為1/10+1/15=1/6,因此需要1÷(1/6)=6天。所以這道題選B。
這道題在計算時其實是有分?jǐn)?shù)計算的,有沒有什么方法可以再簡單一點呢?其實無論設(shè)工作總量為多少都不會影響最終的結(jié)果,為了計算簡便,就要讓效率為整數(shù)。如果效率為整數(shù)就要讓工作總量為時間的倍數(shù),所以也可以設(shè)時間的最小公倍數(shù)為工作總量。設(shè)工程總量為10、15的最小公倍數(shù)30,則甲的工作效率為3,乙的工作效率為2,則甲、乙兩人的合作效率為3+2=5,故甲、乙兩人合作需要30/5=6天。故本題選B。
總結(jié):題目中出現(xiàn)完成同一項工程的多個時間時,可以設(shè)時間的最小公倍數(shù)為工作總量。
例2
甲、乙兩隊完成一項工程的效率比為2∶5。該項工程,若由甲隊先單獨做3天,再由乙隊單獨做4天,最后由甲、乙兩隊合作6天剛好完成。問若由甲隊單獨完成,需要多少天?( )
A.32 B.33 C.34 D.35
【答案】C【解析】這道題中想要求出甲單獨完成要多久就需要知道整個工程的工作量,還有甲的工作效率。題目中出現(xiàn)了甲乙的效率之比,不妨結(jié)合比例設(shè)他們的效率分別為2x、5x,那整個工程的工作量就為3×2x+4×5x+6×(2x+5x)=68x。故甲隊單獨完成需要68x/2x=34天。而這里我們發(fā)現(xiàn)其實到最后我們所設(shè)的x約掉了,所以直接設(shè)工作效率之比為工作效率就好了,因此不妨設(shè)甲、乙兩隊的工作效率分別為2、5,則工作總量為3×2+4×5+6×(2+5)=68,故甲隊單獨完成需要68/2=34天。故本題選C。
總結(jié):題目中出現(xiàn)了工作效率之比,按最簡比設(shè)工作效率。
經(jīng)過上面幾個題目的解析,大家可以發(fā)現(xiàn),只要掌握了方法,工程問題也可以很簡單。








