行測(cè)數(shù)量關(guān)系之利潤(rùn)、牛吃草等問(wèn)題解題技巧
行測(cè)利潤(rùn)概念想明了，根據(jù)題干列個(gè)表
在行測(cè)考試中，數(shù)量關(guān)系部分的利潤(rùn)問(wèn)題是近幾年考查頻率較高也是比較貼近生活實(shí)際的，但是部分題目由于涉及概念較多，在梳理題干信息時(shí)常常沒(méi)有頭緒。那我們?cè)趺茨軌虬杨}干信息梳理的清晰明了呢？其實(shí)我們的方法很簡(jiǎn)單，對(duì)于題目條件比較多且概念比較復(fù)雜的題目，我們不妨用表格把它們整理好再來(lái)找等量關(guān)系計(jì)算。下面通過(guò)題目帶大家來(lái)看看。
例1
甲用1000萬(wàn)元購(gòu)買(mǎi)了一件藝術(shù)品并賣(mài)出，獲利為買(mǎi)進(jìn)價(jià)格的10%，隨后甲用藝術(shù)品賣(mài)出價(jià)格的90%買(mǎi)入一件珠寶，并以珠寶買(mǎi)進(jìn)價(jià)格的九折賣(mài)出。若上述交易中的其他費(fèi)用忽略不計(jì)，甲最終：（ ）
A.盈虧平衡 B.盈利1萬(wàn)元
C.盈利9萬(wàn)元 D.虧損1.1萬(wàn)元
【答案】B【解析】梳理題干的條件列表如下(根據(jù)題干描述順序依次求值列表)：
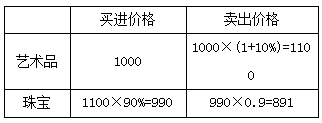
故甲最終盈利(1100-1000)+(891-990)=100+(-99)=1萬(wàn)元，本題選B。
在上述題目當(dāng)中我們發(fā)現(xiàn)涉及到藝術(shù)品和珠寶兩件物品的買(mǎi)進(jìn)和賣(mài)出，為了更好的表達(dá)兩者的價(jià)格變動(dòng)，我們列了兩列表格來(lái)梳理。當(dāng)然有的時(shí)候還是會(huì)涉及到銷(xiāo)量或者多次出售等復(fù)雜的情況，我們也能通過(guò)表格把利潤(rùn)問(wèn)題精細(xì)化。下面再來(lái)看兩道題目：
例2
某企業(yè)生產(chǎn)一種產(chǎn)品，每件成本價(jià)是400元，銷(xiāo)售價(jià)為510元。為進(jìn)一步擴(kuò)大市場(chǎng)，該企業(yè)決定在降低銷(xiāo)售價(jià)的同時(shí)降低生產(chǎn)成本，經(jīng)過(guò)市場(chǎng)調(diào)研，預(yù)測(cè)下季度這種產(chǎn)品每件銷(xiāo)售價(jià)降低4%，銷(xiāo)售量將提高10%。要使銷(xiāo)售利潤(rùn)保持不變，該產(chǎn)品每件的成本價(jià)應(yīng)降低多少元？（ ）
A.7.6 B.10.4 C.13.2 D.16
【答案】B【解析】設(shè)下季度每件成本價(jià)為x元，本季度銷(xiāo)售y件，梳理題干可列表如下：
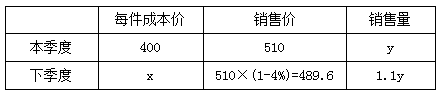
根據(jù)銷(xiāo)售利潤(rùn)保持不變這一等量關(guān)系可得：(510-400)×y=(489.6-x)×1.1y，解得x=389.6，則成本價(jià)降低400-389.6=10.4元，故本題選B。
上述兩道題目均涉及到條件比較多、概念比較復(fù)雜的利潤(rùn)問(wèn)題的概念，單獨(dú)依靠在題干上標(biāo)記的方法，難以理清題干信息，而通過(guò)列表的方式可以將概念間關(guān)系更加直觀、清晰地表示出來(lái)，再通過(guò)題干描述等量關(guān)系或表格內(nèi)概念存在的計(jì)算關(guān)系，最終列方程計(jì)算出答案。
如何解決牛吃草，追及思維要用好
很多同學(xué)認(rèn)為數(shù)量關(guān)系是行測(cè)考試中很難的一部分，所以會(huì)直接放棄，但這是一種比較錯(cuò)誤的認(rèn)識(shí)，實(shí)際數(shù)量關(guān)系有許多基礎(chǔ)的題型是比較簡(jiǎn)單的，并且在近幾年的國(guó)省考中，對(duì)于知識(shí)點(diǎn)的考查還是比較靈活的，所以平時(shí)還是要多積累基礎(chǔ)的題型。今天就給大家介紹數(shù)量關(guān)系里的一個(gè)基礎(chǔ)題型——牛吃草問(wèn)題。
一、牛吃草問(wèn)題的特征
一般牛吃草問(wèn)題的題目中會(huì)出現(xiàn)包含數(shù)量和時(shí)間信息的排比句，例如：“草地上原有一片牧草，草每天是勻速生長(zhǎng)的。放養(yǎng)20頭牛，30天可以吃完；放養(yǎng)25頭牛，20天可以吃完；若放養(yǎng)30頭牛，幾天可以吃完”。題目中出現(xiàn)了3句話都包含牛的數(shù)量和時(shí)間信息，那么這類(lèi)問(wèn)題就可以定義為牛吃草問(wèn)題了。
二、用好追及思維，解決牛吃草問(wèn)題
例1
牧場(chǎng)上有一片青草，每天牧草都勻速生長(zhǎng)。這片牧草可供10頭牛吃20天，或者15頭牛吃10天。問(wèn)：可供25頭牛吃幾天？（ ）
A.3 B.4 C.5 D.6
【答案】C【解析】題目中出現(xiàn)了牛的數(shù)量和吃草時(shí)間相關(guān)的排比句，可以認(rèn)為是牛吃草的問(wèn)題。根據(jù)題目信息可以知道，①牧場(chǎng)上原有一定量的牧草，②牧草每天生長(zhǎng)，③牛每天都在吃草；牛吃這片牧草的過(guò)程，我們可以看作是牛在后邊吃，草在前邊均勻生長(zhǎng)的追及過(guò)程，當(dāng)草被吃完時(shí)便相當(dāng)于“牛追上了草”。根據(jù)追及問(wèn)題公式路程差=速度差×?xí)r間，路程差即為原有的草量，由于是“牛追草”，速度差即為牛每天吃草的速度-草每天草生長(zhǎng)的速度，可以得到：原有草量=(牛每天吃掉的草-每天生長(zhǎng)的草)×?xí)r間；可以假設(shè)每頭牛每天吃的草量為“1”，每天生長(zhǎng)的草量為X，可供25頭牛吃T天，所以原有草量=(10-X)×20=(15-X)×10=(25-X)×T；解方程得X=5；t=5，故本題選擇C項(xiàng)。
通過(guò)上述的題目，我們可以用追及思維去解決牛吃草問(wèn)題；但有些題目中并不是牛去吃草這種表述，但是只要符合“牛吃草”問(wèn)題的特征，那我們也同樣可以用牛吃草的解題思維來(lái)求解，例如下面的這道題目：
例2
某招聘會(huì)上在入場(chǎng)前有人就開(kāi)始排隊(duì)，并且每分鐘來(lái)的人一樣多。從開(kāi)始入場(chǎng)到等候入場(chǎng)的隊(duì)伍消失，若開(kāi)4個(gè)入場(chǎng)口需要30分鐘，開(kāi)5個(gè)入場(chǎng)口需要20分鐘，如果同時(shí)開(kāi)6個(gè)入場(chǎng)口，需要多少分鐘？（ ）
A.8 B.10 C.12 D.15
【答案】D【解析】題目中出現(xiàn)了入場(chǎng)口數(shù)量和時(shí)間相關(guān)的排比句，從外形上看可以認(rèn)為是牛吃草問(wèn)題。根據(jù)題目信息可以知道，入場(chǎng)口每分鐘都在有人入場(chǎng)，相當(dāng)于“牛在吃草”，而每分鐘也會(huì)有人來(lái)排隊(duì)，相當(dāng)于“草在均勻生長(zhǎng)”，入場(chǎng)前的人數(shù)相當(dāng)于“原有的草量”。設(shè)每個(gè)入場(chǎng)口每分鐘入場(chǎng)人數(shù)為1，每分鐘的排隊(duì)人數(shù)為X，所求為T(mén)，根據(jù)入場(chǎng)前的人數(shù)=(入場(chǎng)口數(shù)量-每分鐘來(lái)的人數(shù))×?xí)r間；所以(4-X)×30=(5-X)×20=(6-X)×T；解方程得X=2，T=15；故本題選擇D項(xiàng)。
這就是用追及的思維解決牛吃草的問(wèn)題，大家學(xué)會(huì)了嗎？建議大家在備考期間多多練習(xí)，熟練掌握這類(lèi)問(wèn)題，希望對(duì)大家的備考有所幫助。
行測(cè)數(shù)量關(guān)系中用定位法求概率
無(wú)論是在國(guó)家公務(wù)員考試中還是省考里，數(shù)量關(guān)系都是不可分割的一部分，雖然題目量不是特別多，但是想在短時(shí)間里全做對(duì)還是有一定難度的。因此我們就需要利用一些方法去解題，從而節(jié)約自己做題時(shí)間。而在數(shù)量關(guān)系里都會(huì)有一個(gè)章節(jié)“古典概率”，求古典概率很多同學(xué)第一時(shí)間會(huì)想到用公式求解，今天給大家介紹一種快速求解方法——定位法，下面我們一起學(xué)習(xí)下：
一、定位法使用條件：
①古典概率求解概率
②遇到要同時(shí)考慮相互聯(lián)系的元素時(shí)
③無(wú)論第一個(gè)選哪個(gè)位置，不影響后面選擇的可能性。
二、定位法具體步驟：
先固定其中的一個(gè)元素，再考慮另外一個(gè)元素的可能狀態(tài)，接下來(lái)我們通過(guò)幾個(gè)例題去感受下。
經(jīng)典例題
【例題1】一張紙上畫(huà)了5排共30個(gè)格子，每排格子數(shù)相同，小王將1個(gè)紅色和1個(gè)綠色棋子隨機(jī)放入任意一個(gè)格子(2個(gè)棋子不在同一格子)，則2個(gè)棋子在同一排的概率：（ ）
A.不高于15% B.高于15%但低于20%
C.正好為20% D.高于20%
【答案】B【解析】答案選擇B選項(xiàng)。解析：方法一，將2個(gè)不同顏色的棋子隨機(jī)放入30個(gè)格子中，樣本總數(shù)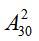
。5排共有30個(gè)格子，每排有6個(gè)格子，則2個(gè)不同顏色的棋子在同一排，樣本數(shù)為
。故經(jīng)計(jì)算2個(gè)棋子在同一排的概率為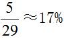
。
方法二，5排共有30個(gè)格子，則每排有6個(gè)格子。先從30個(gè)格子中任選1個(gè)安排紅色棋子，此時(shí)還剩下29個(gè)空格子。若想2個(gè)棋子在同一排，則綠色棋子只能挑選紅色棋子所在排剩余5個(gè)格子中的一個(gè)，則2個(gè)棋子在同一排的概率為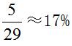
。
【例題2】某單位工會(huì)組織橋牌比賽，共有8人報(bào)名，隨機(jī)組成4隊(duì)，每隊(duì)2人。那么小王和小李恰好被分在同一隊(duì)的概率為( )：
【答案】A【解析】假設(shè)小王已經(jīng)分好隊(duì)，剩下7個(gè)位置小李可以選擇，即總的樣本數(shù)為7，要想和小王一隊(duì)，只有一種情況，即所求事件的樣本數(shù)為1，故兩人被分在同一隊(duì)的概率是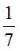
。
通過(guò)上面兩個(gè)題目對(duì)比大家可以發(fā)現(xiàn)在做古典概率題目的時(shí)候有時(shí)候公式求解會(huì)稍微復(fù)雜一點(diǎn)，這個(gè)時(shí)候如果我們能判斷出來(lái)符合定位法的使用條件，就可以利用定位法快速解題。所以希望各位同學(xué)能夠多加練習(xí)，爭(zhēng)取在做題的時(shí)候能夠?qū)W會(huì)利用定位法解題。
“一副撲克牌”玩轉(zhuǎn)行測(cè)最不利原則問(wèn)題
行測(cè)數(shù)量關(guān)系考察內(nèi)容廣泛，題型靈活多樣，讓很多考生在備考時(shí)束手無(wú)策。實(shí)際上，只要把握住每種題型的特征和解題原則，以不變應(yīng)萬(wàn)變，數(shù)量關(guān)系問(wèn)題就可迎難而解。比如，我們有時(shí)會(huì)遇到這樣一類(lèi)問(wèn)題，題干中會(huì)出現(xiàn)“至少.....才能保證...”這樣的字眼，這類(lèi)問(wèn)題我們稱(chēng)之為最不利原則問(wèn)題。今天帶著大家了解最不利問(wèn)題其中的奧秘。
1.何為“最不利”
最不利，就是最倒霉，最壞的情況。舉個(gè)例子：假設(shè)手里有一把鎖，10把鑰匙，其中只有一把鑰匙能打開(kāi)這把鎖。最幸運(yùn)的情況，我們?cè)囈淮尉涂梢源蜷_(kāi)鎖。而最壞的情況呢？需要把所有鑰匙都試過(guò)，即10次，才能把鎖打開(kāi)。
2.題型特征
題干中出現(xiàn)“至少......才能保證...”
3.解題原則
最不利情況數(shù)+1
例題精講
一副完整的撲克牌共計(jì)54張(包含大小王)，其中A、J、Q、K分別對(duì)應(yīng)點(diǎn)數(shù)1、11、12、13。
【例題1】至少抽出( )張才能保證一定有2張牌花色相同？
【答案】7【解析】一副撲克牌有4種花色，黑桃、紅桃、梅花、方塊。外加，大小王各一張。如果想保證有兩張牌花色相同，考慮最不利的情況，首先取出不滿(mǎn)足題意的大小王兩張，接下來(lái)，如果我們?cè)偃∫粡垼赡苁呛谔摇Ｏ乱粡垼欢鼙ＷC是黑桃嗎？不能，可能是紅桃。接著取，下一張，一定能保證是黑桃或者紅桃嗎？不能，可能是梅花。下一張一定能保證是黑桃，紅桃，或者梅花嗎？不能，可能是方塊。而此時(shí)我們?cè)俪橐粡埮疲瑹o(wú)論是哪一種花色，必然存在有種花色是2張牌。
因此，要保證有2張花色相同，考慮最不利情況，需要先取出特殊元素(大小王2張)，然后，四種花色每一種都取1張牌，最后再抽一張即可，即抽2+4+1=7(張)。
【例題2】至少抽出( )張才能保證一定有3張牌點(diǎn)數(shù)相同？
【答案】29【解析】一副撲克牌有1-13共13種點(diǎn)數(shù)，外加，大小王各一張。考慮最不利的情況，即先取出不滿(mǎn)足題意的大小王兩張，再將每種點(diǎn)數(shù)(共13種)各取2張，此時(shí)再抽一張牌，這一張一定是13種點(diǎn)數(shù)中的某一種，就構(gòu)成了3張牌點(diǎn)數(shù)相同，即抽2+2×13+1=29(張)。
綜上可知，解決最不利原則問(wèn)題，重點(diǎn)需要找到最不利的情況，而最不利情況就是最倒霉的，最壞的情況。希望各位考生把握住這一點(diǎn)，快速破題，加油！
