行測數(shù)量關(guān)系技巧
多者合作問題你學(xué)會了嗎
工程問題在公務(wù)員行測考試中是常考的題型之一，也是比較容易得分的題型，而在工程問題中有一類常見題型——多者合作問題，這一類題目一般是涉及到多個合作主體，合作完成某一項工程或幾項工程。首先我們應(yīng)該明確合作效率=各效率的和，其次工作總量=各部分工作量之和。
一、已知多個主體完工時間，將工作總量設(shè)為多個完工時間的最小公倍數(shù)
【例題】某項工程，甲施工隊單獨干需要30天才能完成，乙施工隊需要40天才能完成。甲、乙合作干了10天，因故停工10天，再開工時甲、乙、丙三個施工隊一起工作，再干4天就可全部完工。那么，丙隊單獨干需要大約( )天才能完成這項工程？（ ）
A.21 B.22 C.23 D.24
【答案】B【解析】已知多個主體完工時間，通過特值法設(shè)工作總量為甲乙完工時間的最小公倍數(shù)120，由工作效率=工作總量÷工作時間可得，甲的效率為4，乙的效率為3，設(shè)丙的工作效率為x，則工作總量為：10×(3+4)+4×(3+4+x)=120，解得x=5.5，則丙單獨完成該工程，需要120÷5.5≈21.8天，即需要22天，故本題選B。
二、已知多個主體效率關(guān)系時，根據(jù)效率關(guān)系將效率設(shè)為最簡比的數(shù)值
【例題】甲工程隊與乙工程隊的效率之比為4：5，一項工程由甲工程隊先單獨做6天，再由乙工程隊單獨做8天，最后由甲、乙兩個工程隊合作4天剛好完成，如果這項工程由甲工程隊或乙工程隊單獨完成，則甲工程隊所需天數(shù)比乙工程隊所需天數(shù)多多少天？（ ）
A.3 B.4 C.5 D.6
【答案】C【解析】根據(jù)題干甲乙工程隊的效率之比為4：5，直接設(shè)甲、乙工程隊效率分別為4和5，則總工作量=6×4+8×5+4×(4+5)=100，甲單獨完工需要100÷4=25天，乙單獨完工需要100÷5=20天，所求為25-20=5天。故本題選C。
三、已知多個主體效率相同時，設(shè)每個主體的效率為1
【例題】一批零件，有3臺效率相同的機器同時生產(chǎn)，需用10天完成。生產(chǎn)了2天后，車間臨時接到工廠通知，這批零件需要提前2天完成，若每臺機器的效率不變，需要再投入多少臺相同的機器？（ ）
A.1 B.2 C.3 D.4
【答案】A【解析】根據(jù)題干描述3臺機器效率相同，將每臺機器每天的工作效率設(shè)為1，則工作總量為1×3×10=30，生產(chǎn)兩天后，剩余的工作量為30-1×3×2=24，又需要提前2天完工，則剩余工作量的完工時間就是10-2-2=6，因此剩余工作每天的工作效率為24÷6=4，由于每臺機器每天效率為1，故需要再投入1臺機器。故本題選A。
不定方程如何快速求解
計算問題是行測考試當中每年必考的題型，而不定方程又是計算問題當中常考的一類知識點。實際上，只要掌握一定的解題方法，不定方程也是可以快速求解的。不定方程是指當未知數(shù)的個數(shù)多于獨立方程的個數(shù)時，這樣的方程就稱為不定方程，比如5x+6y=42，3x+2y+10z=52，這類題具體要怎么快速求解呢。
方法一 代入排除法：把選項代入題干當中，得出正確答案。
【例題】7x+9y=55，已知x，y為正整數(shù)，則x的值是：( )
A.2 B.4 C.5 D.7
【答案】B【解析】代入A選項，x=2時，即7×2+9y=55，9y=41，則y不是正整數(shù)，排除；代入B選項，x=4，即7×4+9y=55，9y=27，y=3，符合題干要求x，y為正整數(shù)；同理代入C，D求出y發(fā)現(xiàn)不符合題干要求，故本題選B。
方法二 整除特性：未知數(shù)的某個系數(shù)與常數(shù)之間存在非“1”的公約數(shù)。
【例題】3x+7y=33，已知x，y為正整數(shù)，則x+y=( )
A.11 B.10 C.8 D.7
【答案】D【解析】對于這一道題我們發(fā)現(xiàn)帶入四個選項都去試驗并排除錯誤選項會浪費時間，那我們可以在這個基礎(chǔ)上找到一些方法快速地排除或確定某選項。觀察常數(shù)項33和未知數(shù)x的系數(shù)3存在公約數(shù)3，即3x為3的倍數(shù)，33為3的倍數(shù)，故7y為3的倍數(shù)，而7不是3的倍數(shù)，所以y為3的倍數(shù)，當y為3的時候，x為4符合題意，則x+y=7，故本題選D。
方法三 奇偶性：未知數(shù)前的系數(shù)為一奇一偶。
【例題】雙十一期間小王在網(wǎng)上買了16元一袋的紙巾、10元一支的牙刷和7元一瓶的洗手液若干，共花了156元，如果他買的每一樣物品數(shù)量都不相同。紙巾數(shù)量最多而洗手液最少，那么他買的牙刷數(shù)量比洗手液多幾個？（ ）
A.1 B.2 C.3 D.4
【答案】A【解析】設(shè)買紙巾、牙刷、洗手液的數(shù)量分別為x、y、z，則16x+10y+7z=156(x>y>z)，由于16x、10y和156都為偶數(shù)，所以可知z必須為偶數(shù)，代值檢驗，當z=2時，16x+10y=142，化簡為8x+5y=71，8x為偶數(shù)，71為奇數(shù)，則5y為奇數(shù)，5為奇數(shù)，則y為奇數(shù)，又因為y>z，z=2，則y最小為3，當y=3時，x=7，符合題意，牙刷數(shù)量比洗手液多1個。故本題選A。
方法四 尾數(shù)法：未知數(shù)前的系數(shù)以“0”或“5”為結(jié)尾。
【例題】已知周某生日的月份數(shù)乘以2，加上10，再把和乘以5，加上他家人數(shù)，結(jié)果是143。如果周某家人數(shù)不到10人，則他的生日在幾月？（ ）
A.9 B.10 C.11 D.12
【答案】A【解析】設(shè)周某生日的月份數(shù)和周某家人數(shù)分別為x，y，則有5×(2x+10)+y=143，整理得10x+y=93。10x的尾數(shù)為0，93的尾數(shù)為3，所以y的尾數(shù)為3。由于y<10，那么y只能取3，則x=9。即周某生日在9月。故本題選A。
巧設(shè)未知數(shù)列方程
在行測數(shù)量關(guān)系中，計算問題是無疑高頻考點之一了，利用方程法解決計算問題是我們在平時練習(xí)過程中經(jīng)常會遇到的，然而在同一道題目中，所設(shè)未知數(shù)不同、設(shè)法不同，可以列出很多種不同的等量關(guān)系，但在解方程過程中計算難度卻天差地別。
【結(jié)合分母設(shè)未知數(shù)】
【例題】某班學(xué)生在一次考試中，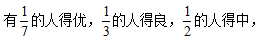
得中的人數(shù)比得優(yōu)、得良的人數(shù)之和多2人。
在這個例子中存在的等量關(guān)系應(yīng)該不難發(fā)現(xiàn)，就是得中的人數(shù)-得優(yōu)、得良的人數(shù)=2。如果將總?cè)藬?shù)設(shè)為x，從而就能表示出得優(yōu)的人數(shù)為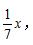
良的人數(shù)
列出方程之后大家會發(fā)現(xiàn)出現(xiàn)多個分數(shù)，求解過程中需要進行通分，相當于要多進行一步計算，那么為了避免復(fù)雜計算，不妨結(jié)合多個分數(shù)的分母，設(shè)總?cè)藬?shù)為42x(42為2、7、6的最小公倍數(shù))，那么得優(yōu)的人數(shù)為6x，得良的人數(shù)為14x，得中的人數(shù)為為21x，從而得到方程：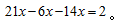
以上根據(jù)同樣條件列出的等量關(guān)系，在求解過程中難度高下立判，所以如果題干出現(xiàn)多個分數(shù)，且都是占某個整體的比重時，我們可以結(jié)合條件，先將分母最小公倍數(shù)求出來再進行設(shè)未知數(shù)列式。
【結(jié)合比例關(guān)系列方程】
如果題干中出現(xiàn)一些比較明顯的比例關(guān)系時，可以結(jié)合比例系數(shù)設(shè)方程，具體通過例2進行說明：
【例題】某高校藝術(shù)學(xué)院分音樂系和美術(shù)系兩個系別，已知學(xué)院男生人數(shù)占總?cè)藬?shù)的30%，且音樂系男女生人數(shù)之比為1∶3，美術(shù)系男女生人數(shù)之比為2∶3。問音樂系和美術(shù)系的總?cè)藬?shù)之比為多少？
A.2∶1 B.3∶2 C.3∶1 D.5∶4
【答案】A【解析】本題已知音樂系男女人數(shù)比為1∶3，可以結(jié)合比例關(guān)系設(shè)音樂系男女人數(shù)分別為x和3x，同理，結(jié)合美術(shù)系男女生人數(shù)之比為2∶3，設(shè)美術(shù)系男女人數(shù)分別為2y和3y。由學(xué)院男生人數(shù)占總?cè)藬?shù)的30%可得等量關(guān)系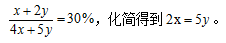
題目所求為音樂系和美術(shù)系的總?cè)藬?shù)之比，即求4x∶5y=10y∶5y=2∶1，根據(jù)選項可知，故本題選A。
快速解決不定方程問題之賦值法
行測考試數(shù)量關(guān)系類題目考察的比較多。不定方程也屬于近年來比較常見的一類題目，那么怎么把不定方程問題做的又快又好呢？下面就帶大家來學(xué)習(xí)其中的一種方法——賦值法。
首先，未知數(shù)的個數(shù)多于獨立方程的個數(shù)，這樣的方程(組)我們稱之為不定方程，例如：
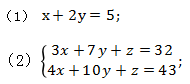
那我們今天學(xué)習(xí)的方法，主要是針對于第二種形式的方程組進行求解，下面我們通過一道例題來說明。
【例題1】甲、乙、丙三種貨物，如果購買甲3件、乙7件、丙1件需花3.15元；如果購買甲4件、乙10件、丙1件需花4.2元，那么購買甲、乙、丙各一件需要花多少元錢？（ ）
A.1.05 B.1.4 C.1.85 D.2.1
【答案】D【解析】根據(jù)題意，可以設(shè)甲1件為x元、乙1件為y元、丙1件為z元，得到一個方程組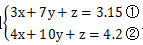
，由于方程組含三個未知數(shù)，但只有兩個獨立方程，所以x，y，z可能有多組解，想要求解“x+y+z”為多少，我們可以采取以下兩種方法。
方法一：通過兩個式子整體運算，整理出x+y+z。可以將式①×3-式②×2恰好得到“x+y+z=1.05”，即A選項。
方法二：由方程組我們是可以得到無數(shù)組的解，但題目是單選題，意味著x+y+z的答案是唯一的，所以可以通過任意一組解來確定這個整體的值。為了方便計算，我們不妨假設(shè)系數(shù)最復(fù)雜的未知數(shù)y=0，可以得到方程組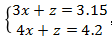
，不難解出x=1.05、z=0，可得“x+y+z=1.05+0+0=1.05”，故本題選D。
對比以上兩種方法，在實際考試中如果想用第一種辦法，需要我們有較強的數(shù)字敏感，仔細認真的觀察每個方程的系數(shù)特點；而方法二操作起來會更簡單，考場上也不會浪費我們太多時間，這就是我們今天主要學(xué)習(xí)的賦值法。使用時大家要注意，只有在求整體時我們才用賦值法，想求其中某一個量具體值時是不適用的，解題時可以將系數(shù)最復(fù)雜的未知數(shù)設(shè)為零，再聯(lián)立剩下的方程求解即可。
【例題2】木匠加工2張桌子和4張凳子共需要10個小時，加工4張桌子和8張椅子需要22個小時。如果他加工桌子、凳子和椅子各10張，共需要多少個小時？（ ）
A.47.5 B.50 C.52.5 D.55
【答案】C【解析】設(shè)木匠加工1張桌子、1張凳子、1張椅子所用時間分別為x、y、z小時，根據(jù)題意有2x+4y=10，4x+8z=22，令x=0，可解得y=2.5，z=2.75，則所求為(0+2.5+2.75)×10=52.5小時。
