行測數(shù)量關系備考
貨物如何集中
近年來公考的分數(shù)呈現(xiàn)了內卷似的直線式提升，每年的入面成績都在不斷地刷新新高。因此，大家不但要投入更多的精力和時間進行復習準備，同時也要講究方法，提升學習效率。下面向大家介紹一種解題方法——貨物集中。
【例題】在一條公路上每隔10公里有一個倉庫，共有5個倉庫，一號倉庫存有10噸貨物，二號倉庫存有30噸貨物，三號倉庫存有20噸貨物，五號倉庫存有15噸貨物，四號倉庫是空的。現(xiàn)在要把所有的貨物集中存放在一個倉庫里，如果每噸貨物運輸1公里需要0.5元運輸費，則集中放在哪個倉庫中運輸總費用最低？（ ）
A.一號 B.二號 C.三號 D.五號
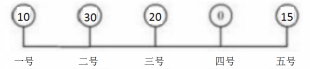
【答案】B【解析】在這道題目當中，可以將選項涉及到的4種情況分別計算出來，并進行比較得出。
如果集中到一號倉庫，運輸總費用為：30×10×0.5+20×20×0.5+15×40×0.5=650元；
如果集中到二號倉庫，運輸總費用為：10×10×0.5+20×10×0.5+15×30×0.5=375元；
如果集中到三號倉庫，運輸總費用為：10×20×0.5+30×10×0.5+15×20×0.5=400元；
如果集中到五號倉庫，運輸總費用為：10×40×0.5+30×30×0.5+20×20×0.5=850元。
經(jīng)過比較可知，集中到二號倉庫，運輸總費用最低。
這道題目也可以利用“支點法”進行判斷：在任意兩個倉庫之間確定一點，記為支點，計算支點兩側貨物的累計重量，由輕的一端向重的一端集中，不用考慮距離和單位距離運費。根據(jù)上述方法，如果將支點確定一號倉庫與二號倉庫之間，那么左側的累計重量為10，右側的累計重量為30+20+15=65，左側比右側輕，因此向移動；如果將支點確定二號倉庫與三號倉庫之間，那么左側的累計重量為10+30=40，右側的累計重量為20+15=35，右側比左側輕，因此向移動左側。因此，可以確定為二號倉庫，故本題選B。
通過上面這道題的分析大家不難發(fā)現(xiàn)，只要是在直線上分布若干倉庫，要把所有的貨物集中存放在一個倉庫里，并且要使運輸總費用最低，都可以利用支點法進行判斷，并且在判斷時只需考慮支點兩側累計重量的大小，由輕向重移動，而不需要考慮其他因素，會使得判斷過程更加簡潔，計算量較小。
“公式法”快速解答行測利潤的相關問題
利潤問題是行測數(shù)量關系考題中常見的一種題型。這類題型往往難度不大，但多數(shù)考生對于利潤問題往往只能夠使用最基本的方程法來進行解答，倘若時間比較緊張便會放棄這一類題目。其實許多利潤問題是可以通過一些基本的公式來快速解答的，下面一起來探索一下這把快速解題的鑰匙。
一、對基本公式“利潤=售價-成本”的應用
【例題】某商品按照定價出售，每個可獲利60元。按定價打八折出售10個所獲得的利潤，與按定價每個減價30元出售15個所獲得的利潤相同。該商品的定價為多少元？（ ）
A.75 B.80 C.85 D.90
【答案】A【解析】根據(jù)利潤問題中的基本公式“利潤=售價-成本”，當成本不變時，我們發(fā)現(xiàn)售價降低多少，利潤也會降低多少。因此，當售價降低30元，利潤也會降低30元，變?yōu)?0-30=30元/個。售出15個，共計獲利15×30=450元。由題可知，打八折售出10個所獲利潤也為450元，因此，打八折售出一個的利潤為450÷10=45元/個。與原來相比，單個的利潤由60元降為45元，下降了15元，所以，售價也應下降15元。具體來看，售價由原售價變?yōu)榱嗽蹆r的0.8倍，所以售價下降了原售價的0.2倍。即：0.2×原售價=15，解得，原售價為15÷0.2=75元。
二、對基本公式“總利潤=單利×銷售量”的應用
【例題】某新款手機上市時的單價是2598元，銷售一段時間后，廠家采取降價促銷的策略，手機單價直降300元，于是每月的銷量提升為原來的2倍，每月利潤提升為原來的1.5倍，則該款手機的成本價是( )元。
A.1698 B.1598 C.1498 D.1398
【答案】D【解析】根據(jù)利潤問題中的基本公式“總利潤=單利潤×銷售量”，從題目中我們看到銷售量變成了原來的2倍，而總利潤只變?yōu)樵瓉淼?.5倍，說明，單利變成了原來的0.75倍。具體來看，售價下降了300元，因此單利也下降的300元；而單利由原來的單利變?yōu)樵瓎卫?/span>0.75倍，下降了原單利的0.25倍。因此0.25×原單利潤=300，解得原單利潤為300÷0.25=1200元，進而可以得到成本應等于原售價2598元減去原單利1200元，即1398元。
通過以上幾道題目的展示，相信考生對利潤問題的解題思路有了一些新的認識，在此之上考生可以多加練習，以便更好地掌握它，并在考場上發(fā)揮這種方法的作用。
啃下行測數(shù)量關系這塊“硬骨頭”
首先我們在心態(tài)上要擺正，不要去恐懼數(shù)學。事實上大多數(shù)的數(shù)量關系題目，是根據(jù)我們小初高的題目變來的。千萬不要害怕，不可能所有題目都非常的難，大多數(shù)題目只是“巧”而已，只要肯學，至少是能攻克幾個題目的。接下來談談學習方法。在這里我們可以分三個階段進行：
第一階段：搞懂題目怎么做
所謂的搞懂，不是去記公式，而是自己去推導解題的過程。比如工程問題，自己去推導工作效率比會讓我得到什么結果，工作總量又如何設合適等等。其實很多題目，可以用列方程的方法解決，但是很多同學覺得列方程很LOW，但是方程在數(shù)量關系問題當中實在是太重要了，一定要強化好。諸如此類的基礎理論一定要學扎實，一定要砸瓷實。這個過程可以稱之為打基礎，大約需要十到十五天的時間。
第二階段：整理解題方法
在初步掌握了方法之后，再對各類題型進行適當?shù)胤诸惪梢宰屪约旱乃悸犯忧逦１热绻こ填悊栴}、行程問題等。分類之后可以尋找兩大類之間的相同之處，比如上述兩個問題就有“時間=總量/效率”，把路程看為工作總量，速度看為工作效率，同樣適用該公式。總之需要大家對理論的理解要特別深入，多舉一反三，多思考，這個階段大概需要五到十天。
第三階段：大量刷題練習
練習又可以分為兩個小階段，第一個階段是分類練習，第二個階段是綜合練習。分類練習就是針對各種類型的題目反復練習，鞏固自己擅長的，彌補自己不足的，大約會用掉十天到十五天；第二個階段綜合練習，可以每天隨機選取一套試卷練十個題，不要多練，十個題，不論做對做錯，都要進行多角度解析，清空思維誤區(qū)。這個過程可以一直持續(xù)到考試前三天。
總體而言，數(shù)量關系不是一個啃不動的硬骨頭，大家要靜下心，一步步來，相信最終都會有所突破！
多者合作不擔憂 設立特值解千愁
工程中的多者合作問題在行測考試中屢見不鮮，但考生往往由于時間緊張或者題目材料過長(一般超過三行)，從而對該類題目選擇放棄，導致失分。但該類題目一旦理清思路，求解過程會很輕松。所以對于此類問題要盡可能地去做。特值法可以很好的為大家提供解題思路，在后續(xù)的解題過程中不迷茫。
工程問題涉及的公式：工作總量=工作效率×工作時間，即W=Pt
特值法的應用
一、題目中出現(xiàn)多個完成工作的時間，將工作總量設為特值，特值設為時間的最小公倍數(shù)；
二、題目中出現(xiàn)或者利用已知條件可求多者效率之比，將效率設為特值，效率之比為多少，特值設為多少。
以上為設特值的兩種情況，下面通過題目展示其具體應用。
【例題1】某項工程，甲工程隊單獨施工需要30天完成，乙工程隊單獨施工需要25天完成。甲隊單獨施工了4天后，改由兩隊一起施工，期間甲隊休息了若干天，最后整個工程共耗時19天完成，問甲隊中途休息了幾天？（ ）
A.1 B.3 C.5 D.7
【答案】D【解析】題目中出現(xiàn)“甲工程隊單獨施工需要30天完成，乙工程隊單獨施工需要25天完成”，有兩個完成工作的時間，將工作總量W設特值，設為30、25的最小公倍數(shù)150，可以求得甲的效率為5，乙的效率為6。題目中描述，“甲隊單獨施工了4天，最后整個工程共耗時19天”，可以推出乙工作了19-4=15天，那么乙完成的工作量為6×15=90，則甲完成的工作量為150-90=60，完成以上工作量甲需工作60÷5=12天，已知整個工程共耗時19天，則甲休息了19-12=7天。故本題選D。
【例題2】手工制作一批元宵節(jié)花燈，甲、乙、丙三位師傅單獨做，分別需要40小時、48小時、60小時完成。如果三位師傅共同制作4小時后，剩余任務由乙、丙一起完成，則乙在整個花燈制作過程中所投入的時間是：（ ）
A.24小時 B.25小時 C.26小時 D.28小時
【答案】A【解析】題目中出現(xiàn)“單獨做，分別需要40小時、48小時、60小時完成”，有三個完成工作的時間，將工作總量W設特值，設為40、48、60的最小公倍數(shù)240，可以求得三位師傅的效率，甲的效率為6，乙的效率為5，丙的效率為4，“三位師傅共同制作4小時”完成的工作量為(6+5+4)×4=60，剩余任務由乙、丙一起完成，還需(240-60)÷(5+4)=20個小時，則整個過程需要投入4+20=24個小時。故本題選A。
【例題3】一項工程由甲、乙、丙三個工程隊共同完成需要22天，甲隊工作效率是乙隊的二分之三倍，乙隊3天的工作量是丙隊2天工作量的三分之二。三隊同時開工，2 天后，丙隊被調往另一工地，那么甲、乙再干多少天才能完成該工程？（ ）
A.20 B.28 C.38 D.42
【答案】C【解析】題目中出現(xiàn)“甲隊工作效率是乙隊的二分之三倍，乙隊3天的工作量是丙隊2天工作量的三分之二”，由此可以得到甲乙的效率之比為3：2，乙丙的效率之比為4：9，則甲乙丙三者的效率之比為6：4：9，則可以假設甲的效率為6，乙的效率為4，丙的效率為9，那么工作總量W=(6+4+9)×22=418，“三隊同時開工2天”完成的工作量為(6+4+9)×2=38，剩下的工作量為418-38=380，還需甲乙工作380÷(6+4)=38天。故本題選C。
通過以上三道題目的分析，想必大家對于多者合作的問題已經(jīng)有所了解，可以多做一做相關的問題，熟能生巧。
整除法巧解計算問題
數(shù)量關系是行測考試中令許多考生感到頭疼的部分，它的考查方式靈活、難度相對較高，而考場上答題時間緊張，所以數(shù)量關系題目經(jīng)常被考生舍棄。考生要想在時間緊題量大的數(shù)量關系中拿到高分，就必須在備考階段熟練掌握一些特定題型的解題技巧。在眾多技巧中整除作為一種題型特征明顯、計算思路簡單的解題技巧，廣大考生在備考時一定要確保能靈活運用。
一般題干中文字表述有“倍”、“每”、“平均”、“整除”或數(shù)據(jù)中出現(xiàn)小數(shù)、分數(shù)、百分數(shù)、比例時，考生可以結合題干中的計算關系和選項設置判斷能否使用整除法。下面我們就結合典型例題詳細給大家介紹一下整除的應用環(huán)境和方法。
【例題1】苗苗有一堆草莓，樂樂也有一堆草莓。苗苗的草莓五個五個地數(shù)，最后剩兩個，七個七個地數(shù)，最后還是剩兩個；樂樂的草莓五個五個地數(shù)，最后剩四個，六個六個地數(shù)，最后剩三個。已知苗苗比樂樂多8個草莓，則苗苗的草莓數(shù)為( )。
A.87 B.92 C.102 D.107
【答案】D【解析】由題意可知，苗苗的草莓數(shù)減去2是既是5的倍數(shù)又是7的倍數(shù)，即苗苗的草莓數(shù)減2是35的倍數(shù)，只有D項符合，故本題選D。
總結：整除法是一種排除錯誤選項的方法，當發(fā)現(xiàn)所求數(shù)據(jù)具有整除特性，可根據(jù)這一特點迅速選出正確選項。
【例題2】幼兒園的老師將122顆糖分發(fā)給全班的小朋友，分發(fā)完后發(fā)現(xiàn)有
的小朋友有兩顆糖，有3個小朋友有3顆糖，其他的小朋友都只有1顆糖。問全班共有多少個小朋友？（ ）
A.57 B.73 C.87 D.92
【答案】C【解析】由“
的小朋友有兩顆糖”，可知全班小朋友的人數(shù)是3的倍數(shù)，排除B、D。代入A項，若全班共有57個小朋友，則小朋友中有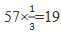
人分到了兩顆糖，57-19-3=35人分到1顆糖，共需要19×2+3×3+35=82顆糖，與122顆矛盾，排除A項。故本題選C。
總結：根據(jù)整除特性判斷選項時若只能排除部分錯誤選項，剩余選項則需要代入驗證確定正確答案。
【例題3】高校某專業(yè)70多名畢業(yè)生中，有96%在畢業(yè)后去西部省區(qū)支援國家建設，其中去偏遠中學支教的畢業(yè)生占該專業(yè)畢業(yè)生總數(shù)的20%，比任職大學生村官的畢業(yè)生少2人，比在西部地區(qū)參軍入伍的畢業(yè)生多1人，其余的畢業(yè)生選擇去國有企業(yè)西部邊遠崗位工作。問去國有企業(yè)西部邊遠崗位工作的畢業(yè)生有多少人？（ ）
A.23 B.26 C.29 D.32
【答案】B【解析】由題干可知，“70多名畢業(yè)生”說明畢業(yè)生人數(shù)為71~79的某個整數(shù)。“有96%在畢業(yè)后去西部省區(qū)支援國家建設”，96%化簡成最簡分數(shù)是24/25，說明西部支援人數(shù)占畢業(yè)生人數(shù)的24/25，可知畢業(yè)生人數(shù)是25的倍數(shù)，即75人，則畢業(yè)后去西部支援國家建設的有96%×75=72人，其中去中學支教、任職村官、參軍入伍的分別有20%×75=15人、15+2=17人、15-1=14人，所以去國有企業(yè)西部邊遠崗位工作的畢業(yè)生有72-15-17-14=26人。故本題選B。
總結：整除特性除了可排除錯誤選項外，有時還可將題干中的未知條件轉化為已知條件。題干條件中若存在已知取值范圍的未知整數(shù)條件(如例3中“70多名畢業(yè)生”)，可先根據(jù)題干中能體現(xiàn)整除特性的數(shù)據(jù)(小數(shù)、分數(shù)、百分數(shù)、比例)確定該未知整數(shù)符合取值范圍的具體值，再以此為已知條件求解問題。
綜上所述，考生可以抓住整除的題型特征多加練習，養(yǎng)成善于發(fā)現(xiàn)整除關系思維習慣，提高自己的答題速度。
