行測數(shù)量關系難點題目解題技巧
行測利潤問題——牢抓等量關系
利潤問題在各省考和國考中屢見不鮮，在2022年國考中再次考了三題，說明這類題型非常重要，在此為大家講解這類題目的技巧。
理論介紹
利潤問題公式較多，需要我們熟記各個公式，而解決利潤問題就是基于各個公式的基礎上找題目中的等量關系，而等量關系在不同的題目中大同小異，先尋找等量關系，再抓住等量關系尋找所需的量，合理設置未知數(shù)列式來解即可。
例題1
企業(yè)列出500萬元設備采購預算，如用于購買x臺進口設備，最后剩余20萬元。經(jīng)董事會研究后，決定購買質(zhì)量更高的同類國產(chǎn)設備，單價僅為進口設備的75%。當前預算可購買x+3臺，最后剩余5萬元。問國產(chǎn)設備的單價在以下哪個范圍內(nèi)？（ ）
A.不到30萬元/臺 B.30~40萬元/臺之間
C.40~50萬元/臺之間 D.50萬元/臺以上
【答案】C
【解析】“企業(yè)列出500萬元設備采購預算，如用于購買x臺進口設備，最后剩余20萬元”也就是給了500萬減去購買進口設備的錢數(shù)等于20萬這樣一個等量關系，購買設備的金額需要用設備臺數(shù)x乘進口設備的單價，那不妨假設進口設備的單價為a萬元/臺，那可以列式為：500-xa=20，又說“決定購買質(zhì)量更高的同類國產(chǎn)設備，單價僅為進口設備的75%”那國產(chǎn)設備的單價即為0.75a。“當前預算可購買x+3臺，最后剩余5萬元”也就是說500萬減去購買國產(chǎn)設備的金額等于5萬，那么同理我們來列式：500-(x+3)×0.75a=5，問題問國產(chǎn)設備的單價在以下哪個范圍內(nèi)？求的是0.75a。我們回到式子中，有兩個方程有兩個未知數(shù)，可以求解出結果，整理求解得到0.75a=45，結合選項選擇C。
例題2
為降低碳排放，企業(yè)對生產(chǎn)設備進行改造，改造后日產(chǎn)量下降了10%，但生產(chǎn)每件產(chǎn)品的能耗成本下降了50%，其他成本和出廠價不變的情況下每天的利潤提高了10%。已知單件利潤=出廠價-能耗成本-其他成本，且改造前產(chǎn)品的出廠價是單件利潤的3倍，則改造前能耗成本為其他成本的：（ ）
【答案】B
【解析】梳理一下題干，“設備進行改造，改造后日產(chǎn)量下降了10%”假設改造前的日產(chǎn)量為a，那改造后的就為0.9a。又說“生產(chǎn)每件產(chǎn)品的能耗成本下降了50%，其他成本和出廠價不變”說明成本就分為能耗成本、其他成本。能耗成本下降50%，假設之前的能耗成本為b，那之后的能耗成本就為0.5b。其他成本和出廠價不變的情況下，每天的利潤提高10%，也就是說有現(xiàn)在每天的利潤=原來每天利潤×(1+10%)這樣一個等量關系，而每天的利潤就應該等于日產(chǎn)量乘單件利潤，改造前后的日產(chǎn)量都已經(jīng)表示出來，所以需要尋找改造前后的單件利潤。而題目中給了一個關于單件利潤=出廠價-能耗成本-其他成本的等式，又說改造前產(chǎn)品的出廠價是單件利潤的3倍，假設之前的單件利潤為c，那之前的出廠價就為3c，根據(jù)等式可得：其他成本=出廠價-能耗成本-單件利潤，即為3c-b-c=2c-b。而改造后其他成本和出廠價不變，那改造后其他成本也為2c-b，出廠價也為3c，那么我們想要的改造后的單件利潤就能表示出來，為3c-0.5b-(2c-b)=c+0.5b，關于每天利潤的等量關系就可以表示為：0.9a(c+0.5b)=ac×1.1。最后問改造前能耗成本為其他成本的多少，即
那簡單整理下方程，發(fā)現(xiàn)等式兩邊都有a，可以約掉，整理得到0.2c=0.45c，再觀察下所求的為2c和b的關系，將0.2c=0.45b，整理為2c=4.5b帶進去約分，就得到
結合選項，選B。
知識小結
我們會發(fā)現(xiàn)利潤問題公式會有很多，其實公式多也就意味著等量關系會有更多，入手點更多，我們在選擇入手點時可以選擇一些也復合概念，比如例題2，以每天利潤=日產(chǎn)量×單件利潤這個復合概念來列式。當然只要把握好核心觀念找等量關系，勤加練習類似題型，會更快掌握此類題型。
行測統(tǒng)籌問題指導之空瓶換水
近年來，統(tǒng)籌問題已成為行測考試中的“新寵兒”，例如在我們?nèi)粘Ｉ钪薪?jīng)常遇到的空瓶換水、貨物集中、排隊取水等。面對這類問題，我們該如何合理安排，從而更高效地辦事呢？這其實就是我們要在統(tǒng)籌問題中去解決的。而空瓶換水問題作為統(tǒng)籌問題中的一類，各位考生總是對此心有余悸。接下來將通過兩道例題帶領大家一起來突破這道難關。
概念
空瓶換水，指的是給出n個空瓶可以換1瓶水的規(guī)則，問現(xiàn)有的空瓶最多可以換多少瓶水，或者要想喝到一定數(shù)量的水，問最少需要購買多少瓶水等類似的問題。
考法
1.直接套用規(guī)則：已知規(guī)則和空瓶數(shù)，求最多能喝到的瓶數(shù)。
例1：一商店規(guī)定4個礦泉水空瓶可以換1瓶礦泉水，現(xiàn)有27個礦泉水空瓶，則最多可以換( )瓶礦泉水。
A.6 B.7 C.8 D.9
【答案】D【解析】當?shù)V泉水瓶數(shù)量較小的時候，我們可以按規(guī)則一步一步地進行兌換。但在實際考試過程中，這種方法不僅浪費時間而且容易在兌換過程中出現(xiàn)差錯，這并不能滿足我們解決行測問題的快、準原則。那我們該如何去計算呢？下面政華教育為大家提供一種更好的解題思路。
根據(jù)題干中的“4個礦泉水空瓶換1瓶礦泉水”，我們用等式來表示就可以寫成：4個礦泉水空瓶=1瓶礦泉水=1個礦泉水空瓶+1份水(一份水不包括空瓶)，可以得：3個礦泉水空瓶=1份水。現(xiàn)在我們用27÷3=9，即27個礦泉水空瓶通過兌換最多可以得到9瓶水。答案選D。
總結：通過這個例題發(fā)現(xiàn)，在解決空瓶換水問題時，我們只需要找到空瓶與水的代換關系，即n個空瓶可以換1份水，然后用總的空瓶數(shù)m來除以n就可以得到最終答案。
2.間接套用規(guī)則：已知規(guī)則及喝到的瓶數(shù)，求至少應買多少瓶水。
例2：商店做活動，8個空瓶可以換一瓶水，小芳這個月一共喝了65瓶水，那么她花錢買的至少有多少瓶水？（ ）
A.56 B.57 C.58 D.59
【答案】B【解析】首先我們需要注意，小芳喝的這65瓶水包括小芳她自己花錢買的和通過兌換得到的。因此，如果我們設小芳花錢買了x瓶水，并且題干中的“8個空瓶可以換一瓶水”，我們用等式來表示可以寫成：8個礦泉水空瓶=1瓶礦泉水=1個礦泉水空瓶+1份水(一份水不包括空瓶)，可以得：7個礦泉水空瓶=1份水。則小芳通過兌換可以得到x÷7瓶水，因此可以得到x+x÷7=65，解得x=56.875，即至少買56.875瓶水加上兌換的才能保證小芳這個月喝了65瓶，而礦泉水瓶數(shù)只能是整數(shù)，因此在不小于56.875的整數(shù)里選擇最小的57，答案選B。
總結：當我們已知規(guī)則及喝到的瓶數(shù)，求至少應買多少瓶水時，我們只需要利用換水規(guī)則列方程求解即可。只不過需要注意的是，當未知數(shù)解出來為非整數(shù)時，我們需要向上取整。
學到這里，大家對空瓶換水問題是不是很清晰明了了呢？在遇到空瓶換水問題時，我們只需抓住空瓶換水的規(guī)則便可以快速解題。希望通過今天的分享能為各位考生在備考路上起到一定的助力作用。
你知道A事件發(fā)生的概率是多大嗎
概率問題是國省考行測中的重要題型，也讓很多考生為之頭疼，是大家的痛點和難點，但解決這類題型的思路和方法相對固定，有很強的規(guī)律性。今天就帶大家學習概率問題的求解方法，讓大家遇到這類問題能夠很好地解決。
公式
概率研究某一事件發(fā)生的可能性大小。在行測考試中常考古典概率(又稱等可能事件概率)，強調(diào)事件具有有限性以及每個基本事件發(fā)生的可能性相等。求解A事件發(fā)生的概率：
想得知概率為多大，就得找到“總事件包含的等可能樣本數(shù)”以及“A事件包含的等可能樣本數(shù)”，找到這二者，概率問題也就迎刃而解。
實戰(zhàn)演練
例1：小王從編號分別為1、2、3、4、5的5本書中隨機抽出3本，那么，這3本書的編號恰好為相鄰三個整數(shù)的概率為多少？（ ）
【答案】C【解析】所求概率為多少，根據(jù)概率計算公式，找到“總事件所包含的等可能樣本數(shù)”以及“A事件包含的等可能樣本數(shù)”。總事件為從5本書中隨機抽出3本，故總事件有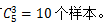
所求A事件為選出3本書的編號是相鄰的三個整數(shù)，符合條件的有1、2、3，2、3、4，3、4、5，有3個樣本。故所求概率為
。選C。
例2：從1、2、3、4、5中隨機抽取3個數(shù)，問這3個數(shù)之和至少能被其中一個數(shù)整除的概率是多少？（ ）
A.10% B.30% C.60% D.90%
【答案】D【解析】所求概率為多少，根據(jù)概率計算公式，找到“總事件所包含的等可能樣本數(shù)”以及“A事件包含的等可能樣本數(shù)”。總事件為從5個數(shù)中隨機抽出3個數(shù)，故總事件有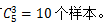
所求A事件為3個數(shù)之和至少能被其中一個數(shù)整除，由于任何整數(shù)都能被1整除，故可以分類討論，當抽取的3個數(shù)中含有1時，還得從剩下的4個數(shù)中抽取2個，每一個基本事件都能滿足3個數(shù)之和至少能被其中一個數(shù)整除的條件，故樣本數(shù)為
當抽取的3個數(shù)中不含有1時，就得從剩下的2、3、4、5中抽取3個數(shù)，樣本數(shù)較少，可以一一討論，分別為2、3、4，2、3、5，2、4、5，3、4、5，抽取的3個數(shù)為2、3、4時，和為9，能被3整除，滿足條件，抽取的3個數(shù)為2、3、5時，和為10，能被2和5整除，滿足條件，抽取的3個數(shù)為2、4、5時，和為11，不滿足條件，抽取的3個數(shù)為3、4、5時，和為12，能被3和4整除，滿足條件，故樣本數(shù)為3個；因此所求A事件的樣本數(shù)為6+3=9個。所求概率為
選D。
小結：解決古典概率問題，得明確總事件以及所求的A事件是什么，從而求出其對應的基本事件樣本數(shù)，帶入求解得到概率。
希望各位小伙伴通過上面兩道能夠掌握古典概率在具體題目中的運用，對做題帶來一定的啟發(fā)。
用特值法解決工程問題中的多者合作
很多同學認為行測數(shù)量關系做起來很花時間且有一定的難度，從而不大愿意去花時間拿分，在這里給大家分享一種可以拿分的題型，即工程問題下的多者合作題型。工程問題是考場上常見的一種題型，這種題型一般情況下都是用方程來解，但速度不夠快，如何能夠做到做對的同時又保證做題的效率呢？接下來給大家具體介紹一下它的用法。
基本公式
工作總量=工作效率×工作時間
基本方法
1.當題目中出現(xiàn)多個完成工作時間，設工作總量為特值，一般為時間的最小公倍數(shù)。
例1：錄入員小張和小李需要合作完成一項錄入任務，這項任務小李一人需要8小時，小張一人需要10小時。兩人在共同工作了3個小時后，小李因故回了趟家，期間小張一直在工作，小李返回后兩個人又用了1個小時就完成了任務。在完成這項任務的過程中，小張比小李多工作了幾個小時？（ ）
A.1 B.1.5 C.2 D.2.5
【答案】A【解析】設工作總量為40(8和10的最小公倍數(shù))，則小李的工作效率為5，小張的工作效率為4。由題意可知，兩人合作了3+1=4小時，完成工作量(4+5)×4=36，則小張單獨工作(40-36)÷4=1小時，即小張比小李多工作了1小時。
2.當題目中出現(xiàn)效率比，設效率比為特值。
例2：甲工程隊與乙工程隊的效率之比為4∶5，一項工程由甲工程隊先單獨做6天，再由乙工程隊單獨做8天，最后由甲、乙兩個工程隊合作4天剛好完成，如果這項工程由甲工程隊或乙工程隊單獨完成，則甲工程隊所需天數(shù)比乙工程隊所需天數(shù)多：( )。
A.3天 B.4天 C.5天 D.6天
【答案】C【解析】設甲、乙工作效率分別為4、5，則這項工程的任務量為4×6+5×8+(4+5)×4=100。甲工程隊單獨完成需要100÷4=2天，乙工程隊單獨完成需要100÷5=20天，所求為25-20=5天。
3.當題目中出現(xiàn)多人或多物，設效率為1。
例3：修一條公路，假設每人每天的工作效率相同，計劃180名工人1年完成，工作4個月后，因特殊情況，要求提前2個月完成任務，則需要增加工人多少名？（ ）
A.50 B.65 C.70 D.60
【答案】D【解析】設每名工人每月的工作量為1，則全部工作量為180×12，工作4個月完成工作量180×4。設要想提前2個月，則需要增加工人x名，則有180×4+(180+x)×(12-4-2)=180×12，解得x=60。
相信大家通過上面三個例題，能對多者合作下的特值法有一定的理解，特值法的應用范圍還是能夠保質(zhì)保地去解決題目，建議接下來各位同學在做題的過程當中能去使用這種方法，真正掌握這種做題的方法，從而提高自身的做題水平。
