行測數量關系常考題型解題技巧
行測數量關系：巧解直角三角形，穩(wěn)定結構穩(wěn)定拿分
公務員考試中幾何問題考查的頻率越來越高，其中解直角三角形則是重中之重。直角三角形作為大家從小就開始接觸的知識點，想必對于它是十分親切熟悉的，因而也成為我們數量關系做題當中的優(yōu)先選擇。那么我們要怎么依據直角三角形的相關知識進行解題呢？
想要能夠求解出直角三角形的相關題目，兩個相關的知識點是大家需要掌握的。
一、勾股定理：勾股定理指的是直角三角形中兩直角邊的平方和等于斜邊的平方，常見的勾股數有3、4、5；6、8、10；5、12、13；
二、把握含30°和45°角的兩個特殊直角三角形的比例關系：含30°的直角三角形中，30°角對應的直角邊的長度是斜邊的一半，各邊之比為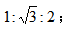
含45°的直角三角形中，各邊之比為
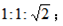如下圖所示：
學習了直角三角形的相關知識點，以后再碰到幾何問題，我們就可以借助題目條件構造直角三角形，利用勾股定理以及含30°和45°角的直角三角形的各邊比例關系來解題，接下來我們就通過兩個例題來看看如何求解吧!
例題展示
例題1
甲地在乙地的正東方，在丙地的正南方。甲、乙之間距離為2.1千米。小張從甲地騎車直線前往丙地，回程時以相同速度直線前行乙地再直線返回甲地，回程時的路程比去程長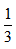
問：甲丙之間的距離在以下哪個范圍內？
A.不到5千米 B.5-6千米 C.6-7千米 D.超過7千米
【答案】D【解析】根據題意，我們可以根據“上北下南，左西右東”的原則畫出甲、乙、丙之間的位置關系，如下圖所示
因為甲在乙的正東，在丙的正南，正東和正南構成直角，因而甲、乙、丙三地的連線構成了直角三角形，甲乙之間距離為2.1千米，小張先從甲地到乙地，回程時是由丙→乙→甲，根據回程時的路程比去程長
我們可以得到，
設甲丙之間的距離為3x，那么丙乙+甲乙=4x，丙乙=4x-2.1，根據直角三角形中勾股定理可得
超過7千米。故本題選D。
例題2
一艘巡邏艇航行至海面某處時，得知正北方向20海里處有一漁船發(fā)生故障，就立即指揮港口的救援艇前往該處營救。已知發(fā)生事故處位于港口北偏東45°的方向上，港口位于巡邏艇北偏西30°的方向上。港口到出事地點的距離為：
【答案】B【解析】根據題意畫出巡邏艇、故障發(fā)生處、港口之間的位置關系，如圖所示，B點為巡邏艇所在位置，C點為事發(fā)地點，A點為港口
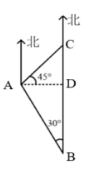
根據題意可知，BC=20海里，∠B=30°可構造直角三角形來解題，過點A作AD垂直于BC，交BC于點D，則∠CAD=90°-45°=45°，設CD=x海里，則AD=CD=x海里，在直角三角形ADB中，由∠B=30°可知，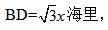
BD+CD=BC，
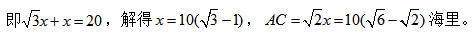故選B。
通過以上兩個題目我們可以看到，只要把握住勾股定理和兩個特殊直角三角形三邊的比例關系這“一定理兩特殊”，許多幾何問題都可以通過構造直角三角形迎刃而解，大家也可以通過練習更多題目從而能夠對于直角三角形的知識點進行靈活應用。
行測年齡問題不用愁，表格梳理來解憂
爭分奪秒巧復習，勤學苦練創(chuàng)佳績。正在備戰(zhàn)公考的小伙伴們，你們是否已經做好披荊斬棘的準備？還是苦于找不到自己的練習之路，正處于漫漫摸索的階段呢？無論進度如何，想必大家都有一些困惑，例如行測考試中的數量關系部分，數學題目難度較高、耗時較長，那如何盡可能在短時間內得出正確結果？今天，帶大家認識一種數量關系題型——年齡問題。
年齡問題是研究兩個或多個個體之間年齡變化和關系的問題。題目條件易于理解，但數據變化較多，易于混淆，因此，我們在解決這類問題時，通常采用“列表法”來梳理并分析題干，再依據等量關系列方程即可。
那具體該如何列表，請看以下例題：
例題1
一家三口，父親的年齡比母親大10歲，2009年，父親的年齡是兒子的9倍，2016年，母親的年齡是兒子的3倍，則母親的出生年份為：
A.1973年 B.1975年 C.1983年 D.1985年
【答案】C解析】假設2016年兒子的年齡為x，則母親的年齡為3x，父親的年齡為3x+10。
根據題意可得：9×(x-7)=3x+10-7，解得x=11，母親2016年為33歲，出生于2016-33=1983年。故選C。
由此可見，我們只需將不同年份下所有人的年齡梳理在表格中，年齡問題就可迎刃而解了。同時小伙伴們也要注意，其實年齡問題中有一個“隱藏福利”，那就是“年份差=個人增加或減少的年齡”，如2009年到2016年，三人的年齡都增加了七歲，同學們可不要忽略這個條件呀!
讀到這里，大家是不是都有所收獲了呢？那就快練習一下吧!
例題2
2018年父親年齡是女兒年齡的6倍，是母親年齡的1.2倍。已知女兒出生當年(按0歲計算)母親24歲，則哪一年父母年齡之和是女兒的4倍？
A.2036 B.2039 C.2042 D.2045
【答案】B【解析】假設2018年女兒的年齡是x歲，則2018年父親的年齡是6x歲，母親的年齡是6x÷1.2=5x歲。
已知女兒出生當年(按0歲計算)母親24歲，即母親比女兒大24歲，有5x-x=24，解得x=6，故可得2018年三人年齡并填在表中。再過n年，父母年齡之和是女兒的4倍，有36+30+2n=4×(6+n)，解得n=21，所以在2018+21=2039年父母年齡之和是女兒的4倍。故選B。
行測數量關系：未知數多不要慌，工程問題用特值
在行測考試數量關系部分中，工程問題是一種常考題型，解決這類題目的核心是利用工作總量、效率和時間三者之間的關系
列方程解決；在往年考察的題目中往往會出現(xiàn)多者合作完成工作的情況，其中涉及未知數較多，此時我們可以根據題干的描述，巧妙地利用特值法來解決這類題目，接下來就帶領大家一起學習一下最常考察的三種特值法解工程問題的題型。
一、已知多個主體完工時間時，可設工作總量為完工時間的公倍數
例題1
一項工程，甲單獨做24天可以完成，甲、乙合作15天可以完成，乙、丙合作10天可以完成。現(xiàn)甲、乙、丙三人合作，3天后有一人有事離開，問最少還需要多少天完工？
A.5 B.6 C.7 D.8
【答案】A【解析】題干中給出了三個完工時間，那么我們設工作總量為24、15和10的最小公倍數120，則甲的效率為120÷24=5，甲、乙的合作效率為120÷15=8，乙、丙的合作效率為120÷10=12，則乙的效率為8-5=3，丙的效率為12-3=9。三人合作3天完成的工作量為3×(5+12)=51，剩余工作量為120-51=69，一人離開后要想工作時間最少，則讓效率高的兩人繼續(xù)工作，即甲、丙繼續(xù)工作，還需69÷(5+9)≈4.9天，因此最少還需要5天可以完工。故本題選A。
二、題干直接給出效率比，可設效率為比例值
例題2
甲、乙、丙三個工程隊的工作效率之比為2∶3∶6。一項工程，乙工程隊單獨施工需要28天完成。實際施工時，甲工程隊先單獨施工若干天，再由丙工程隊單獨施工，最終也用了28天完成，則甲工程隊完成了工程總量的：
A.30% B.40% C.50% D.60%
【答案】C【解析】題干中直接給出了效率比，那么我們設甲、乙、丙三隊的工作效率分別為2、3、6，則工作總量為3×28=84。設實際工作時甲隊單獨做t天，根據題意有2t+6×(28-t)=84，解得t=21，則甲完成的工作量為2×21=42，故所求為42÷84×100%=50%。故本題選C。
三、題干未給出明確的效率關系，可根據不同工作方式的工作量相等建立等量關系后推出效率關系，再設效率為特值
例3
一批口罩的加工任務，甲單獨加工12天完成。若甲先單獨加工3天，再由乙單獨加工2天，則能完成任務的一半。現(xiàn)甲和乙合作加工若干天后，再由乙單獨加工至完成任務，最終發(fā)現(xiàn)甲、乙合作加工的時間與乙單獨加工的時間相同，則完成該加工任務共用多少天？
A.3 B.4 C.6 D.8
【答案】C【解析】C。根據題意可得，
則甲、乙效率比為2∶3，那么我們設甲和乙的工作效率分別是2和3，則工作總量為12×2=24。設甲、乙合作加工的時間與乙單獨加工的時間都是t天，則(2+3)×t+3t=24，解得t=3，故完成該加工任務共用2×3=6天。故本題選C。
教育希望同學們學習過程中，拿出一些時間有針對性地訓練這類題目，從而拿下這一題型。
