行測數量關系難點題目解題技巧
行測考試中這種概率問題真的不要再錯了——古典概率之定位法
數量關系一直是行測試卷中大家比較頭疼的一類題目。但行測想要拿高分，數量關系題目還是要重點突破的。其中概率問題是考生認為難度較高的題型，因為解題時往往需要用到難度更大的排列組合的相關知識，所以讓概率問題看起來“難上加難”。但是有這樣一種概率問題，如果能夠識別出題型并熟練掌握“定位法”，就能繞開用排列和組合去表示總的等可能樣本數和事件A的等可能樣本數，直接得出最終結果。下面政華公考就用幾道例題帶大家一起來看看關于“定位法”的相關知識以及應用。
基本知識
1.定位法的題型特征：題目中對兩個元素的相對位置有要求，如兩個元素同排、同隊、相鄰等，可以考慮用定位法。
2.定位法的解題步驟：可以先確定一個元素的位置，再考慮另一個元素的位置可能的樣本數(分母)和位置滿足題目要求的樣本數(分子)。
例題1：一張紙上畫了5排共30個格子，每排格子數相同，小王將1個紅色和1個綠色棋子隨機放入任意一個格子(2個棋子不在同一格子)，則2個棋子在同一排的概率：（ ）
A.不高于15% B.高于15%但低于20%
C.正好為20% D.高于20%
【答案】B【解析】題目要求2個棋子放在同一排，是對這2個棋相對位置有要求，可以用定位法解題。假設紅色棋子隨機選擇某個格子，此時還剩下29個空格子，想再選1個格子放綠色棋子，則共有29個位置可以選，但綠色棋子如果想和紅色棋子在同一排，則綠色棋子只能挑選紅色棋子所在那一排中剩余5個格子中的一個，故所求的2個棋子在同一排的概率為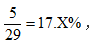
介于15%和20%之間，選擇B。
例題2：某學校舉行迎新篝火晚會，100名新生隨機圍坐在篝火四周。其中，小張與小李是同桌，他倆坐在一起的概率為：（ ）
【答案】C【解析】小張和小李2人要坐在一起，是對這兩個人相對位置有要求，可以用定位法。假設小張隨機選擇某個位置，則小李還有99個位置可以選擇，其中有小張左、右2個位置可以滿足二人相鄰，則所求概率為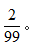
通過以上題目相信大家已經能夠基本了解定位法的解題步驟，希望在以后遇到這類題目時，能靈活應用，快速解決此類題目。
持續(xù)關注政華公考，教你更多解題技巧。
行測數量關系：利潤問題——“買賣中的章法”
“利潤問題”在公考中也是常考題型，也是比較好得分的題型，只要我們能夠理清楚題干描述的各個概念。利潤問題，本質是“買賣”的問題，而“買”“賣”，我們就是要明確買進的情況、賣出的情況，包括買進和賣出的價格、數量，這些都是我們解決利潤問題的必要條件。
例1：服裝店買進一批童裝，按每套獲利40%定價，賣出這批童裝的80%后，按定價的八折將剩下的童裝全部賣出，總利潤比預期減少了560元。問服裝店買進這批童裝花了多少元（ ）？
A.6000 B.8000 C.10000 D.12000
【答案】C【解析】根據題意，實際描述的是購進一批服裝分兩批賣出去的情況。設買進x元/件，共買進y件。列表如下:
總利潤=原利潤-560，1.4x×0.8y+1.12x×0.2y-xy=(1.4x-x)×y-560，解得xy=10000，即所求總花費。答案選C。
例2：某超市購進一批水果，按50%的利潤定價銷售，由于定價比其他超市高，第一天只賣出了總量的10%；第二天打八折促銷，賣出了總量的70%；為了盡快售完，第三天超市在第二天的基礎上打五折促銷，最終全部售完。則這批水果最終：（ ）
A.盈利11% B.虧損11% C.盈利15% D.虧損15%
【答案】A【解析】根據題意，購進水果分三批賣，設購進成本為x元/千克，共購進y千克。整理如下：
最終所獲得的利潤率=(總售價-總成本)÷總成本=(1.5x×0.1y+1.2x×0.7y+0.6x×0.2y-xy)÷xy=0.11。答案選A。
例3：商場銷售A、B兩種成本和定價都相同的商品，A按定價賣出20件后，降價30%賣出40件；B按定價賣出48件后，提價20%賣出12件。商場發(fā)現截至此時，銷售B商品的利潤是銷售A商品利潤的3倍。則每件A商品的成本是定價的（ ）
A.64% B.68% C.70% D.72%：
【答案】B【解析】根據題意，商場銷售A、B兩種商品的情況，A、B進價和定價都相同，分別設為x元/件、y元/件我們可以做出整理。
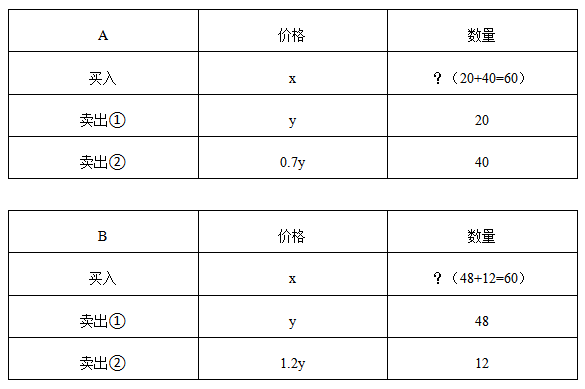
B的利潤是A的3倍，可得：48y+1.2y×12-60x=(20y+0.7y×40-60x)×3；化簡整理得120x=81.6y，則所求x/y=0.68。答案選B。
總結
利潤問題求解，本質就是“買賣”，買入和賣出，列表梳理的方式也能讓我們更清晰更直觀地梳理出條件來，幫助我們更快地解決問題。當然，掌握利潤問題的基本公式也是解決這類問題的前提。
行測數量關系：牢記解題原則，巧解和定最值
和定最值問題是公務員行測考試中的一類常見考點，指的是在幾個數加和一定的情況下求其中某個量的最大(小)值的問題。如將20顆糖果分給5個小朋友，求分得糖果最多的小朋友最多分得了多少顆？
解決和定最值問題需遵循一個基本原則：若求其中某個量的最大值，則讓其他量盡可能小；若求其中某個量的最小值，則讓其他量盡可能大。接下來，政華公考帶著這個解題原則一起來求解以下和定最值的常見題型。
1.求最大量的最大值/最小量的最小值
關鍵點：根據解題原則確定出每一項具體的值，直接相加減即可解題。
例1：6人參加百分制考試，成績總和為400分，已知6人都及格了，成績均為整數且依據成績排名無并列名次，求第一名最多得了多少分（ ）？
A.84 B.90 C.95 D.98
【答案】B【解析】根據解題原則，按照成績從高到低進行排名，要求第一名最多得了多少分，則其他五人得分盡可能少。已知6人都及格了，則排名第六的人最少為60分，由于無并列名次且都為整數，則排名第五的人最少應比排名第五的人多一分，為61分，排名第四的人得62分，排名第三的人得63分，排名第二的人得64分，排名第一的人為所求量設為x，則x+64+63+62+61+60=330，解得x=84。
2.求最大量的最小值/最小量的最大值
關鍵點：根據解題原則確定不了具體量的值，可以構造盡可能接近的數列方程求解。
例2：現有40本故事書分給5個人閱讀，如果每個人得到的書的數量都不相同，那么得到故事書數量最多的人至少可以得到多少本（ ）？
A.10 B.7 C.9 D.11
【答案】A【解析】根據解題原則，要求得到故事書最多的人最少得了多少本，則其他人所得數量盡可能多。設分得故事書最多的人最少分了x本，由于每個人得到的數量都不相同，則所得故事書數量排名第二的人最多應該比排名第一的少一本，為x-1本，排名第三的人得x-2本，排名第四的人得x-3本，排名第五的人得x-4本，則有x+x-1+x-2+x-3+x-4=40，解得x=10。
3.求中間某個量的最大值/最小值
關鍵點：可以根據解題原則確定具體量的先確定具體量，其余的構造盡可能接近的數列方程求解。
例3：假設五個相異正整數和為45，則這五個數中排名第三的最大為多少（ ）？
A.7 B.8 C.10 D.13
【答案】D【解析】根據解題原則，按數字大小從多到少進行排列，要求排名第三的數最大為多少，則讓其他數盡可能小。由于都是相異的正整數，則排名第五的數最小為1，排名第四的數為2，排名第三的為所求數，設為x，排名第二的數最小應該比排名第三的數大1，為x+1，排名第一的數為x+2，則有x+2+x+1+x+2+1=39，解得x=13。
只要牢記解題原則，就能巧解和定最值問題。更多解題技巧，歡迎關注政華公考！
行測數量關系：空瓶巧換水
在致力于全民環(huán)保的21世紀，一些商家為了增強消費者的環(huán)保理念，會推廣諸如“幾個空瓶可以換一瓶水”的活動，由此也衍生出行測中的一個考點—空瓶換水。它是具有技巧性的統籌問題，考查形式相對單一，例如：通過已知的空瓶數量以及兌換原則，讓我們去求解可以喝到多少瓶水。很多同學采用的是一步一步兌換的方法，費時且易出錯，今天政華公考帶大家一起來學習如何巧解此類題目。
例1：某商店為了吸引顧客做一個促銷活動，每3個空汽水瓶可以換一瓶汽水，問：小張共有11個空瓶最多可以喝到幾瓶汽水（ ）？
解析：(1)基本方法：由于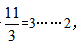
可知能換到3瓶汽水還剩2個空瓶，3瓶汽水喝掉后再加剩余的2個空瓶，可得到5個空瓶。
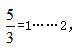能換到1瓶汽水還剩2個空瓶，1瓶汽水喝掉可得到3個空瓶，又能換到1瓶汽水，最終共喝到3+1+1=5瓶汽水。
(2)巧解方法：明確題目中的核心兌換規(guī)則，3個空瓶換1瓶汽水，也就是3空瓶=1瓶水=1空瓶+1份水，即2空瓶=1份水。因此，直接用
最多能喝到5瓶汽水。
【解題方法】直接套用公式——已知規(guī)則及空瓶數，問最多能喝到水的瓶數。
例2：若12個空瓶可以免費換1瓶汽水，現有101個空瓶，最多可以免費喝到幾瓶汽水（ ）？
A.8瓶 B.9瓶 C.10瓶 D.11瓶
【答案】B【解析】明確題目中的兌換規(guī)則，12個空瓶換1瓶水，即12空瓶=1瓶水=1空瓶+1份水，即11空瓶=1份水。因此所求為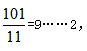
最多能喝到9瓶汽水。
例3：商店開展“7個空瓶換一瓶啤酒”的優(yōu)惠活動。已知張先生在活動促銷期間共喝掉347瓶“紅星”啤酒，問張先生最少買多少瓶啤酒（ ）？
A.296 B.298 C.300 D.302
【答案】B【解析】明確題目中的兌換規(guī)則，7空瓶=1瓶酒=1空瓶+1份啤酒，即6空瓶=1份啤酒。此時設張先生最少需要買x瓶啤酒，則換回酒的份數為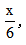
由題可得：
此時需要分析x的取值，x假設為最少，而啤酒的瓶數一定是整數，需要向上取整，因此最少需要買298瓶啤酒，故選擇B選項。
【解題方法】間接套用公式——已知規(guī)則及喝到水的份數，求至少應買多少瓶水。
以上即為空瓶換水的巧解方法。以后解決此類問題時，首先需要明確題目中的兌換規(guī)則，將兌換規(guī)則轉化為a空瓶=b份水的形式，再進行求解即可。此類問題在考試中的考查形式相對來講比較單一，同學們只要明確方法，相信可以輕松解決。
行測數量關系典型題型：牛吃草問題
行測數量關系問題對大部分考生來說都是一個比較頭疼的問題，計算量大，耗時長。那么，怎么在有效時間內快速解決問題呢？今天政華公考就來介紹一下比較經典的牛吃草問題的答題技巧，希望能夠對大家有所幫助。
題型特征
一個典型的牛放牧問題的條件是：假設草在持續(xù)生長，且生長速度固定，不同數量的牛吃掉同一片草地所需的天數不同，求幾頭牛可以吃掉這片草地需要多少天。由于吃的天數不同，草每天都在生長，因此草的存量隨著吃的天數不斷變化。
牛群放牧問題的關鍵在于，這一問題具有隱蔽性。如果每頭牛每天以不同的速度和數量吃草，這個問題就沒有解決辦法。因此，為了確定這一問題，每頭牛每天吃草的速度和數量必須相同。
核心公式
原有草量=(牛每天吃掉的草量-每天生長的草量)×天數
基本思路：假設每一頭牛的吃草速度為1，根據不同的牛吃草列出關于總草量的等量關系式，進而求出我們求的數值。
解題方法
例1：牧場上一片青草，每天牧草都勻速生長。這片牧草可供10頭牛吃20天，或者可供15頭牛吃10天。問：可供25頭牛吃幾天（ ）？
A.2 B.3 C.4 D.5
【答案】D【解析】設每頭牛吃1份草，每天新增加的牧草為x，可供25頭牛吃t天。根據核心公式可得：(10-x)×20=(15-x)×10=(25-x)×t，解得t=5，所以答案選D。
例2：某水庫共有10個泄洪閘，當10個泄洪閘全部打開時，8小時可將水位由警戒水位降至安全水位；只打開6個泄洪閘時，這個過程為24小時，如水庫每小時的入庫量穩(wěn)定，問如果打開8個泄洪閘時，需要多少個小時可將水位降至安全水位（ ）？
A.10 B.12 C.14 D.16
【答案】B【解析】某水庫原有水量相當于原有草量，泄洪閘相當于牛，假設1個泄洪閘的泄水量為1，水庫每小時的入庫量為x。則由牛吃草核心公式可得：(10-x)×8=(6-x)×24=(8-x)×t，解得t=12，故選B。
牛吃草的困難在于草每天都在生長，因此草的數量在不斷變化。因此，解決這些問題的關鍵是找到一種方法，從變化中找到恒定的數量，例如單位時間內每頭牛的草速和原始草量。
牛吃草是一種難度相對適中的題型，大部分題目可能會以不同的形式表現出來，例如例題2水庫放水等，但是整體換湯不換藥。只要理解題目含義，掌握核心公式，找到對應的量，利用核心解題方法，就能解決問題、從容應對。在我們行測考試中，這種解題技巧還有很多，只要掌握之后便能夠更好地應對考試。
