行測(cè)數(shù)量關(guān)系數(shù)學(xué)運(yùn)算技巧
行測(cè)指導(dǎo)：一副撲克牌教你學(xué)會(huì)最不利原則
在行測(cè)考試中，數(shù)量關(guān)系部分的很多題很難在短時(shí)間內(nèi)求得結(jié)果，所以同學(xué)們會(huì)有恐懼心理，但是數(shù)量關(guān)系也是難易結(jié)合的，有些相對(duì)簡(jiǎn)單的題型我們還是可以挑出來(lái)做一下的。今天政華公考跟大家共同來(lái)學(xué)習(xí)一類(lèi)比較簡(jiǎn)單的題型——最不利原則問(wèn)題。
先來(lái)看兩種不同的問(wèn)法，
問(wèn)題1：一副完整的撲克牌，至少抽出多少?gòu)埦陀锌赡艹榈郊t桃K？
問(wèn)題2：一副完整的撲克牌，至少抽出多少?gòu)埐拍鼙ＷC抽到紅桃K？
對(duì)比觀察發(fā)現(xiàn)，兩種問(wèn)法的區(qū)別在于一個(gè)問(wèn)“有可能”，一個(gè)問(wèn)“能保證”。“有可能”強(qiáng)調(diào)可能性，抽出一張就有可能抽到紅桃K，所以問(wèn)“至少…有可能”時(shí)我們考慮的就是最有利的情況。這種問(wèn)法求解起來(lái)比較簡(jiǎn)單。
而“能保證”強(qiáng)調(diào)的是事情百分之百會(huì)發(fā)生，即在運(yùn)氣最差的情況下，也要讓它發(fā)生，就是要從最不利的情況去思考，即最不利原則問(wèn)題。
最不利原則題型特征
題目問(wèn)法出現(xiàn)類(lèi)似“至少…才能保證(就一定)”的表述。
解題方法
利用最不利原則解題，先要分析清楚題目想要達(dá)到的目標(biāo)，再?gòu)谋M量不達(dá)成目標(biāo)的角度去思考，即考慮與成功一線之差的情況，最后再+1來(lái)滿(mǎn)足題目的要求。
例題：從一副完整的撲克牌中，至少抽出多少?gòu)埮疲拍鼙ＷC至少6張牌的花色相同。（ ）
A.21 B.22 C.23 D.24
【答案】C【解析】題目最終的目標(biāo)是想要有6張牌的花色相同，考慮最不利的情況，就是先不讓同一種花色抽出6張牌，每種花色最多先抽5張牌，還有大小王(無(wú)花色)，此時(shí)已經(jīng)抽出了4×5+2=22張牌，未達(dá)成目標(biāo)。但接下來(lái)再抽出一張牌，不管抽出的是什么花色，該種花色的牌已經(jīng)有6張牌了，即達(dá)成了目標(biāo)。所以至少抽出的牌數(shù)為22+1=23張牌，選擇C選項(xiàng)。
【總結(jié)】最不利數(shù)=目標(biāo)數(shù)-1，想要有10張花色相同的牌，每種花色最多先給10-1=9張；想要有7張點(diǎn)數(shù)相同的牌，每種點(diǎn)數(shù)最多先給6張。
練一練
例題：某高校舉辦的一次讀書(shū)會(huì)共有37位學(xué)生報(bào)名參加，其中中文、歷史、哲學(xué)專(zhuān)業(yè)各有10位學(xué)生報(bào)名參加了此次讀書(shū)會(huì)，另外還有4位化學(xué)專(zhuān)業(yè)學(xué)生和3位物理專(zhuān)業(yè)的學(xué)生也報(bào)名參加了此次讀書(shū)會(huì)，那么一次至少選出幾位學(xué)生，將能保證選出的學(xué)生中至少有5位學(xué)生是同一專(zhuān)業(yè)的？（ ）
A.17 B.20 C.19 D.39
【答案】B【解析】想要達(dá)成的目標(biāo)是保證至少有5位學(xué)生是同一專(zhuān)業(yè)的，按照：最不利數(shù)=目標(biāo)數(shù)-1，每個(gè)專(zhuān)業(yè)最多先選4人，其中中文、歷史、哲學(xué)專(zhuān)業(yè)各有10位學(xué)生，先各選4人，化學(xué)專(zhuān)業(yè)共4人，全選出來(lái)，物理專(zhuān)業(yè)有3位同學(xué)，最多選3人，已經(jīng)選出了4×4+3=19人，接下來(lái)再選一個(gè)人，一定中文、歷史、哲學(xué)三個(gè)專(zhuān)業(yè)其中的一個(gè)，則該專(zhuān)業(yè)選出的人數(shù)為5，滿(mǎn)足條件，本題選B。
通過(guò)上述講解，政華公考相信大家對(duì)最不利原則的問(wèn)題有了一定的了解，同學(xué)們要牢記題型特征和解題方法，多加練習(xí)，掌握這種相對(duì)簡(jiǎn)單的題目。
行測(cè)數(shù)量關(guān)系：如何破解古典概率
古典概率在行測(cè)數(shù)量關(guān)系中是一種常考的題型，很多同學(xué)拿到這類(lèi)題目，往往比較頭疼，做題比較慢，一方面是因?yàn)樽鲱}思路不明確，同時(shí)難以確定總事件和A事件，另一方面是因?yàn)樵谟?jì)算總事件和A事件的樣本數(shù)時(shí)需要用到排列組合的知識(shí)，而很多同學(xué)遇到排列組合又會(huì)望而卻步。基于以上兩方面的原因就導(dǎo)致很多同學(xué)做這類(lèi)型題目的時(shí)候，時(shí)間長(zhǎng)，正確率低。接下來(lái)就由政華公考結(jié)合例題帶大家一起學(xué)習(xí)一下如何快速地解決古典概率問(wèn)題。
基本公式
典型例題
例1：某公司將在本周一至周日連續(xù)七天舉辦聯(lián)誼會(huì)，某員工隨機(jī)選擇其中連續(xù)的兩天參加聯(lián)誼會(huì)，那么他在周五至周日期間連續(xù)兩天參加聯(lián)誼會(huì)的概率為：（ ）
【答案】B【解析】根據(jù)題意，總事件是員工從周一至周日中選擇連續(xù)兩天參加聯(lián)誼會(huì)，根據(jù)枚舉法，對(duì)應(yīng)的樣本數(shù)為6；A事件是員工從周五至周日中選擇連續(xù)兩天參加聯(lián)誼會(huì)，對(duì)應(yīng)的樣本數(shù)為2，則所求概率為
故本題選B。
【總結(jié)】解決古典概率問(wèn)題的思路是先找出總事件和A事件分別是什么，再計(jì)算出各自所對(duì)應(yīng)的等可能樣本數(shù)，最后結(jié)合公式進(jìn)行求解。
例2：已知一個(gè)箱子中裝有12件產(chǎn)品，其中2件次品。若從箱子中隨機(jī)抽取2件產(chǎn)品進(jìn)行檢驗(yàn)，則恰好抽到1件次品的概率是：（ ）
【答案】B【解析】根據(jù)題意，總事件是從12件產(chǎn)品中任意抽取2件，此時(shí)若用枚舉法所對(duì)應(yīng)的樣本數(shù)較多，花費(fèi)時(shí)間較長(zhǎng)，故采用組合數(shù)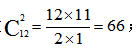
A事件是恰好抽到1件次品，即抽取的兩件產(chǎn)品1件次品，1件非次品，對(duì)應(yīng)的樣本數(shù)為
例3：小明有2盆蘭花和3盆杜鵑，小明打算隨機(jī)拿出2盆送給小紅，則至少有1盆蘭花的概率是：（ ）
【答案】D【解析】根據(jù)題意，總事件是從2盆蘭花和3盆杜鵑中任意選2盆花，對(duì)應(yīng)的樣本數(shù)為
A事件是選擇的兩盆花中至少有一盆是蘭花，其中包括兩類(lèi)情況，一類(lèi)是1盆蘭花1盆杜鵑，對(duì)應(yīng)的樣本數(shù)為
另一類(lèi)是兩盆都是蘭花，對(duì)應(yīng)的樣本數(shù)為1，所以A事件的樣本數(shù)為6+1=7，則所求概率為
故本題選D。
通過(guò)上面三道例題的練習(xí)，政華公考相信大家對(duì)于古典概率問(wèn)題的解題方法也有了一定的認(rèn)識(shí)，為了進(jìn)一步熟練這種題型，還需要同學(xué)們?cè)趥淇贾星诩泳毩?xí)，熟練之后才可以在考場(chǎng)上應(yīng)用自如，幫助我們提高做題的速度。
行測(cè)數(shù)量關(guān)系：利用隔板巧解同素分堆問(wèn)題
排列組合問(wèn)題作為行測(cè)考試中的一個(gè)考點(diǎn)，難度系數(shù)很高，是令很多同學(xué)耗費(fèi)精神的一個(gè)知識(shí)點(diǎn)，但是排列組合類(lèi)的題型中，不乏有一些比較特殊的題型，可以通過(guò)特殊的思維進(jìn)行解決。那么今天政華公考就帶大家來(lái)通過(guò)隔板思維解決相同元素的分堆問(wèn)題。
例1：有10個(gè)相同的蘋(píng)果，分給3個(gè)小朋友，每個(gè)小朋友至少一個(gè)，問(wèn)共有多少種分法？（ ）
A.45 B.36 C.120 D.42
【答案】B【解析】根據(jù)題意，10個(gè)相同的蘋(píng)果分給3個(gè)小朋友，也就是把蘋(píng)果分成3堆。那么將10個(gè)蘋(píng)果排開(kāi)，只需要往蘋(píng)果與蘋(píng)果的空隙之間插入2塊板，就可以分為3堆。因?yàn)槊總€(gè)小朋友至少一個(gè)，所以只能在10個(gè)蘋(píng)果中間的9個(gè)空隙中插入2塊板，因?yàn)榭张c空之間是相同的，改變順序?qū)Y(jié)果沒(méi)影響，用組合數(shù)，答案為
所以答案選擇B。
上述例題就是一個(gè)簡(jiǎn)單的“隔板法解決同素分堆”的題目，就是將相同的東西分給幾個(gè)人，我們?cè)跂|西的中間空隙用板子隔開(kāi)進(jìn)行分堆即可，接下來(lái)一起來(lái)總結(jié)一下可以用隔板法解題的題型特征以及解題公式。
題型特征：把n個(gè)相同元素分給m個(gè)不同的對(duì)象，每個(gè)對(duì)象至少1個(gè)元素，問(wèn)有多少種不同分法的問(wèn)題。1.所要分配的元素必須完全相同(例如10個(gè)相同的蘋(píng)果)。2.每個(gè)對(duì)象至少分到1個(gè)(比如每個(gè)小朋友至少一個(gè))。
解題公式：方法數(shù)共有
了解題型特征以及公式后，那我們來(lái)看看怎么來(lái)靈活地運(yùn)用“隔板法”呢？
例2：把10個(gè)相同的蘋(píng)果分給3個(gè)小朋友，每個(gè)小朋友至少2個(gè)，問(wèn)共有幾種分法？（ ）
A.15 B.21 C.20 D.42
【答案】A【解析】根據(jù)題目，“10個(gè)相同的蘋(píng)果”說(shuō)明相同元素，“分給3個(gè)小朋友”說(shuō)明要分成3堆，但是題目中是“每個(gè)小朋友至少2個(gè)”，與題型特征中“每個(gè)對(duì)象至少1個(gè)”不符，不能直接使用“隔板法”，所以我們要先把“至少2個(gè)”變?yōu)椤爸辽?個(gè)”。如果先給每個(gè)小朋友發(fā)1個(gè)蘋(píng)果，現(xiàn)在蘋(píng)果還剩10-3=7個(gè)，7個(gè)相同分發(fā)給3個(gè)小朋友，每個(gè)小朋友至少1個(gè)，直接使用公式，答案為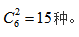
選擇A。
相信大家通過(guò)上述題目的講解，能對(duì)“隔板法”有一定的了解。政華公考建議大家在備考期間需多多練習(xí)，真正做到熟練掌握這類(lèi)問(wèn)題，希望對(duì)于大家的備考能有所幫助。
行測(cè)排列組合別放棄，隔板模型拯救你
排列組合問(wèn)題一直是行測(cè)數(shù)量關(guān)系考查的重點(diǎn)，其題型靈活多變，整體難度較大，讓很多考生望而卻步，很多考生的感覺(jué)是考試年年考，但與“我”無(wú)關(guān)。真的是這樣的嗎？排列組合問(wèn)題就真的不可突破了嗎？難道我們也要和對(duì)手一樣放棄了嗎？其實(shí)不然，排列組合也有很多簡(jiǎn)單的、可掌握的知識(shí)點(diǎn)，今天政華公考就帶大家來(lái)學(xué)一學(xué)其中的一個(gè)題型——隔板模型。
初識(shí)隔板模型
例題：某城市一條道路上有4個(gè)十字路口，每個(gè)十字路口至少有1名交通協(xié)管員，現(xiàn)將8個(gè)協(xié)管員名額分配到這4個(gè)路口，則每個(gè)路口協(xié)管員名額的分配方案有：（ ）
A.35種 B.70種 C.96種 D.114種
【答案】A【解析】題干要求將8個(gè)協(xié)管員名額分配在4個(gè)不同的十字路口，每個(gè)路口至少1名交通協(xié)管員。根據(jù)題干被分配的是協(xié)管員名額，名額不存在差異，可以看成同樣的元素；要求分配給的是4個(gè)十字路口，每一個(gè)路口是不一樣的，可以看成是分給不同的對(duì)象；且題干要求每個(gè)路口至少一個(gè)。所以可以抽象為將8個(gè)相同元素分配給4個(gè)不同對(duì)象，每個(gè)對(duì)象至少分配1個(gè)元素，如下圖：
此時(shí)只需要將8個(gè)相同元素的間隔上插入3個(gè)隔板，即可以將8個(gè)相同元素按照不同數(shù)量分配給了4個(gè)不同對(duì)象。
如按照以上的方式插入隔板的話相當(dāng)于A分2個(gè)元素，B和C分1個(gè)元素，D分4個(gè)元素。隨著隔板所選的3個(gè)間隔的不同，產(chǎn)生不同的數(shù)量分配，但是每一個(gè)對(duì)象至少要分1個(gè)，只能在中間的7個(gè)間隔里選3個(gè)插入隔板。則總方法數(shù)應(yīng)為
故選A選項(xiàng)。
【技巧點(diǎn)撥】把n個(gè)相同的元素分給m個(gè)不同的對(duì)象，每個(gè)對(duì)象至少分1個(gè)元素，則可以理解為隔板模型類(lèi)的題目。其方法數(shù)為
變形突破
如果將n個(gè)相同元素分配給m個(gè)不同對(duì)象，每個(gè)對(duì)象至少為1個(gè)元素，直接帶模型及結(jié)論即可，但是在考試過(guò)程中，我們往往就會(huì)遇到一些變形，我們一起來(lái)學(xué)習(xí)一下吧。
變形一
例題：某城市一條道路上有4個(gè)十字路口，每個(gè)十字路口至少有2名交通協(xié)管員，現(xiàn)將13個(gè)協(xié)管員名額分配到這4個(gè)路口，則每個(gè)路口協(xié)管員名額的分配方案有：（ ）
A.28 B.56 C.72 D.112
【答案】B【解析】題干要求將13個(gè)相同的名額分配在4個(gè)不同的十字路口，每個(gè)路口至少2個(gè)。題干依然是將n個(gè)相同元素分給m個(gè)不同對(duì)象的題目，只是要求變?yōu)榱嗣總€(gè)對(duì)象至少分2個(gè)元素。此時(shí)我們可以考慮先給每個(gè)對(duì)象先分1個(gè)元素，則就能轉(zhuǎn)化成每個(gè)對(duì)象至少1個(gè)的模型。相當(dāng)于將13-4=9個(gè)相同元素分給4個(gè)不同對(duì)象，每個(gè)對(duì)象至少分1個(gè)，即
【技巧點(diǎn)撥】把n個(gè)相同的元素分給m個(gè)不同的對(duì)象，每個(gè)對(duì)象至少分多個(gè)元素時(shí)，先轉(zhuǎn)化成每個(gè)對(duì)象至少分1個(gè)的模型，再利用隔板模型進(jìn)行求解。
變形二
例題：某城市一條道路上有4個(gè)十字路口，現(xiàn)將8個(gè)協(xié)管員名額分配到這4個(gè)路口，則每個(gè)路口協(xié)管員名額的分配方案有：（ ）
A.87種 B.112種 C.165種 D.360種
【答案】C【解析】題干要求將8個(gè)相同的名額分配給4個(gè)不同的十字路口，每個(gè)路口的名額沒(méi)有要求，即有些路口可以分不到。題干依然是將n個(gè)相同元素分給m個(gè)不同對(duì)象的題目，只是要求變?yōu)榱嗣總€(gè)對(duì)象可以分不到(分0個(gè))元素。此時(shí)我們可以考慮先向每個(gè)對(duì)象先“借”1個(gè)元素，則每一個(gè)對(duì)象至少需要將“借”的還回去，就轉(zhuǎn)化成了每個(gè)對(duì)象至少1個(gè)元素的模型。相當(dāng)于將8+4=12個(gè)不同的元素分給4個(gè)不同的對(duì)象，每個(gè)對(duì)象至少分1個(gè)元素，即有
故選C選項(xiàng)。
【技巧點(diǎn)撥】把n個(gè)相同的元素分給m個(gè)不同的對(duì)象，存在某個(gè)對(duì)象可能分不到(分0個(gè))元素。則可先向該對(duì)象先“借”1個(gè)元素，然后即可轉(zhuǎn)換為每個(gè)對(duì)象至少分1個(gè)的模型，再利用隔板模型進(jìn)行求解。
以上即為隔板模型的標(biāo)準(zhǔn)型及其兩個(gè)變式，它本質(zhì)上就是相同元素的分配問(wèn)題，事實(shí)上，我們只需要記住并且理解標(biāo)準(zhǔn)型的定義和結(jié)論，變式題型可舉一反三，通過(guò)先分或先借的方法轉(zhuǎn)換使其滿(mǎn)足每個(gè)對(duì)象至少分1個(gè)元素的條件，再代入公式計(jì)算即可。所以排列組合也有可做的題目，不能全然放棄哦！
行測(cè)數(shù)量關(guān)系：如何應(yīng)對(duì)一元二次函數(shù)求極值
提到與一元二次函數(shù)相關(guān)的問(wèn)題小伙伴們是不是倒吸了一口冷氣呢？大家第一反應(yīng)可能想到的都是復(fù)雜的求根公式，覺(jué)得這類(lèi)題目計(jì)算量大不好求解。但是一元二次函數(shù)求極值作為行測(cè)考試中經(jīng)常會(huì)出現(xiàn)的一類(lèi)題目，究竟有沒(méi)有簡(jiǎn)單有效的方法去解決呢？今天政華公考就帶著小伙伴們一探究竟！
知識(shí)鋪墊
一般式：
函數(shù)圖像及兩根：其圖像是一條關(guān)于
的兩個(gè)交點(diǎn)分別記為
開(kāi)口方向與極值：拋物線的開(kāi)口方向由a的正負(fù)決定，當(dāng)a>0時(shí)，拋物線開(kāi)口向上，則函數(shù)在對(duì)稱(chēng)軸處存在最小值；當(dāng)a<0時(shí)，拋物線開(kāi)口向下，則函數(shù)在對(duì)稱(chēng)軸處存在最大值。
考查形式以及解決方法
1.考查形式
一元二次函數(shù)在考試當(dāng)中經(jīng)常會(huì)結(jié)合利潤(rùn)問(wèn)題以求極值的形式出現(xiàn)。
2.解決方法
因?yàn)楹瘮?shù)圖像的對(duì)稱(chēng)性，所以往往可以將一般式整理為兩項(xiàng)相乘的形式，也就是零點(diǎn)式
令這兩項(xiàng)各自為0，并計(jì)算出函數(shù)式為0時(shí)的兩個(gè)根
，由于圖像對(duì)稱(chēng)的這一性質(zhì)，該平均值位于對(duì)稱(chēng)軸上時(shí)，可以使得一元二次函數(shù)求得最值。
例題展示
例1：某商品的進(jìn)貨單價(jià)為80元，銷(xiāo)售單價(jià)為100元，每天可售出120件。已知銷(xiāo)售單價(jià)每降低1元，每天可多售出20件。若要實(shí)現(xiàn)該商品的銷(xiāo)售利潤(rùn)最大化，則銷(xiāo)售單價(jià)應(yīng)降低的金額是：（ ）
A.5元 B.6元 C.7元 D.8元
【答案】C【解析】
則降低后的銷(xiāo)售單價(jià)為(100-x)元，銷(xiāo)量為(120+20x)件，進(jìn)貨單價(jià)為80元，則總利潤(rùn)y=(100-x-80)×(120+20x)，y=0時(shí)的兩個(gè)根為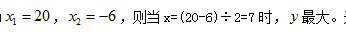
選擇C選項(xiàng)。
例2：某苗木公司準(zhǔn)備出售一批苗木，如果每株以4元出售，可賣(mài)出20萬(wàn)株，若苗木單價(jià)每提高0.4元，就會(huì)少賣(mài)10000株。那么，在最佳定價(jià)的情況下，該公司最大收入是多少萬(wàn)元？（ ）
A.60 B.80 C.90 D.100
【答案】C【解析】設(shè)苗木單價(jià)提高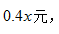
則可賣(mài)出(20-x)萬(wàn)株，此時(shí)收入為y萬(wàn)元，y=(4+0.4x)×(20-x)，令y=0，可解得
則當(dāng)x=(-10+20)÷2=5時(shí)，y取最大值，收入最大為(4+0.4×5)×(20-5)=90萬(wàn)元。選擇C選項(xiàng)。
【點(diǎn)撥】
今天的小知識(shí)你收下了嗎？其實(shí)一元二次函數(shù)的相關(guān)問(wèn)題并沒(méi)有大家想得那么復(fù)雜，只要大家掌握核心關(guān)系，勤加練習(xí)，一定能有所收獲。希望大家能夠在政華公考的幫助下節(jié)省寶貴的時(shí)間呦！
